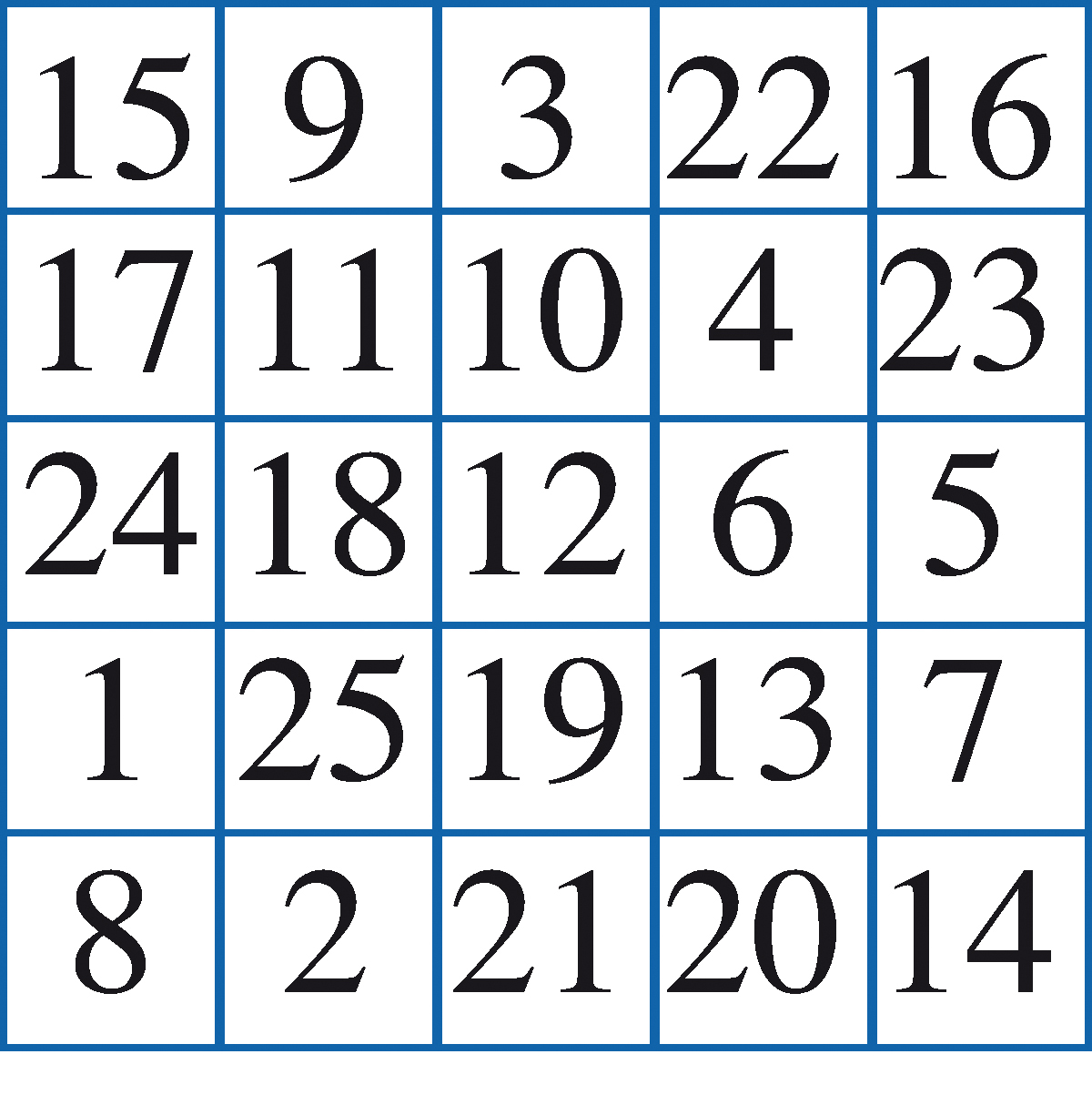
Un carré magique normalest constitué de n2 cases contenant les entiers de 1 à n2 disposés de telle façon que la somme des nombres contenus dans chaque ligne, dans chaque colonne ou dans chacune des deux diagonales soit toujours la même. La somme en question est alors appelée la somme magique. Ci-dessous figure un carré magique normal d’ordre 5, de somme magique 65.
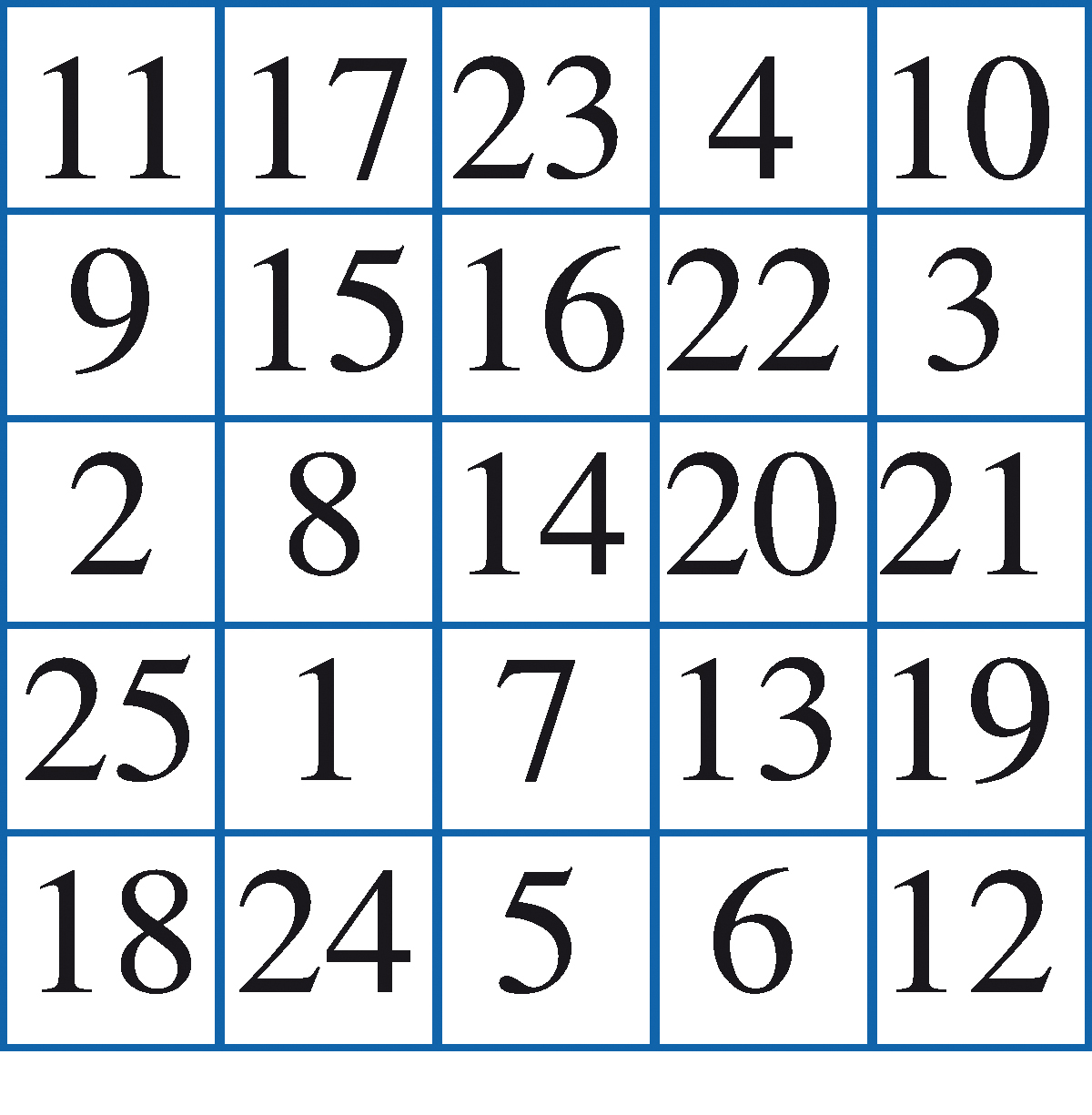
Dans ce carré, remplaçons maintenant chaque nombre par son complément à 26 (dans un carré d’ordre n, on prendrait le complément à n2 + 1). On obtient un nouveau carré magique normal, le dual du précédent.
Appliquons l’opération sur le plus ancien carré magique connu, présent en Chine depuis plus de deux mille ans : le Lo Shu, d’ordre 3 et de somme magique 15. Construisons son dual en remplaçant chaque nombre par son complément à 10.
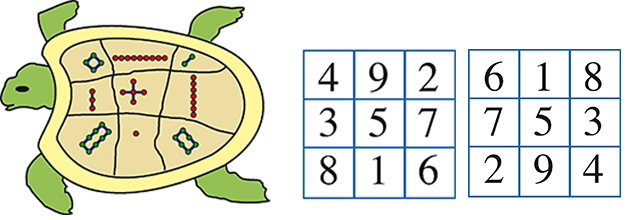
On obtient le même carré, à rotation ou symétrie près ! Le Lo Shu est donc un carré autodual. Rien d’étonnant à cela : le carré magique normal d’ordre 3 est unique, à rotation et symétrie près…
1. Existe-t-il un carré magique d’ordre 5 égal à son dual (à rotation ou symétrie près) ? Si oui, quelles conditions doit-il vérifier ?
Dites-le avec des polygones
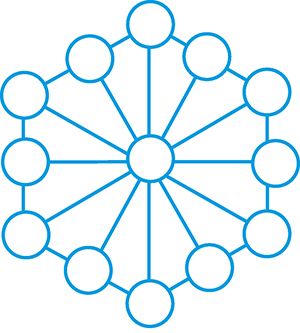
L’univers de la magie arithmétique a exploré bien d’autres figures que le carré. Celle qui suit est un pentagone magique normal, contenant les entiers de 1 à 16 et dans lequel tout alignement de trois nombres a pour somme 30. On construit son dual en remplaçant chaque nombre par son complément à 17.
Le nouveau pentagone est également magique, mais sa somme magique n’est plus la même, elle est ici égale à 21. Les nombres sont en effet répartis en cinq entiers appartenant à une seule somme, cinq entiers appartenant à trois sommes et un entier (au centre) appartenant à cinq sommes. Cette répartition détermine la valeur de la somme magique.
Par ailleurs, le pentagone initial présentait également une somme de cinq nombres, situés sur le cercle en pointillés, égale à la somme magique 30. Le pentagone dual perd cette propriété.
2. Un hexagone magique
Il s’agit avec l’hexagone qui suit de placer les nombres de 1 à 13 dans les disques de telle sorte que la somme des nombres placés dans trois disques alignés soit toujours la même. Existe-t-il une solution ? Si oui, qu’en est-il de la configuration duale ?