Problème 1
Dans un cryptarithme, deux lettres différentes correspondent à deux chiffres différents, et aucun nombre ne commence par 0. À vous de compléter cette addition ! La solution est unique.
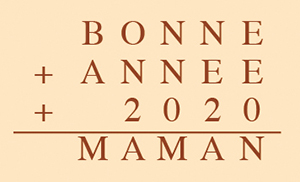
Problème 2
On a écrit les entiers 1, 2, 3… n dans cet ordre de gauche à droite dans la première ligne d’une grille carrée n × n, puis les entiers n + 1, n + 2 … 2n sur la deuxième ligne, et ainsi de suite, jusqu’à n2, placé dans la case en bas à droite de la grille. La figure montre une petite portion de la grille, où seuls les nombres placés dans deux cases, 997 et 7 060, ont résisté aux dommages du temps.
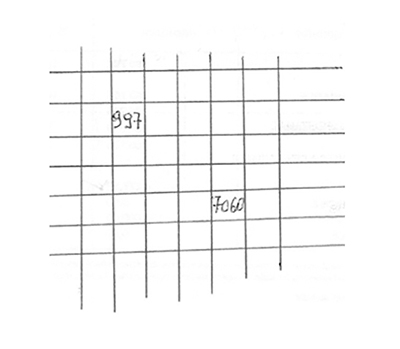
Quelle est la dimension n de la grille ?
Problème 3
Trouver un carré parfait dont la somme des chiffres est 2 020.

