Georg Cantor a établi que l’ensemble des nombres rationnels (ceux que l’on peut écrire sous la forme de fractions d’entiers) est dénombrable, tout comme l’ensemble des nombres entiers naturels. Pour cela, parmi toutes les façons de les ordonner, il a imaginé une façon de ranger les nombres rationnels, ou plutôt leurs écritures fractionnaires.
La méthode de l’argument diagonal

L’ingénieuse méthode trouvée par Cantor consiste à ranger les écritures fractionnaires comme s’il s’agissait des couples de coordonnées des points à coordonnées entières d’un quart de plan. On associe par exemple le point de coordonnées (4 ; 3) à la fraction 4 / 3. Ensuite, Cantor propose une façon de parcourir cet ensemble de points qui permet de les lister tous : 1 / 1, 2 / 1, 1 / 2, 1 / 3, 2 / 2, 3 / 1, 4 / 1, 3 / 2, 2 / 3, 1 / 4, 1 / 5… (suivant les flèches du diagramme). On peut donc numéroter ces points, ce qui revient à construire une bijection entre les entiers naturels et les écritures de fractions d’entiers. Remarquez que plusieurs écritures fractionnaires représentent le même nombre rationnel : 1 / 2 = 2 / 4 = 3 / 6 = …
On prouve ainsi que l’ensemble des nombres rationnels strictement positifs est un ensemble dénombrable. On prouverait que la propriété est vraie pour l’ensemble de tous les rationnels en ajoutant 0 au diagramme et en faisant suivre chaque fraction par son opposé : 0, 1 / 1, – 1 / 1, 2 / 1, – 2 / 1, 1 / 2, – 1 / 2…

Neil Calkin (né en 1961).

Herbert Saul Wilf (1931–2012).
On peut imaginer bien d’autres façons de ranger les nombres rationnels. En voici une, publiée en 2000 par les mathématiciens américains Neil Calkin et Herbert Wilf. Celle-ci a l’avantage d’« éviter les doublons », c’est-à-dire de ne pas lister les écritures différentes d’un même nombre rationnel.
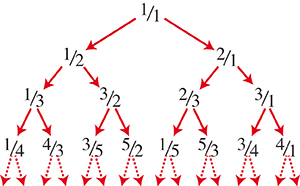
L’idée de ces deux chercheurs est de ranger les fractions dans un arbre de la façon suivante. Chaque nombre rationnel de l’arbre engendre deux nombres : à gauche, un nombre rationnel ayant le même numérateur que son nombre géniteur et, pour dénominateur, la somme des deux nombres de la fraction qui l’engendre ; à droite, un nombre ayant le même dénominateur que son nombre géniteur et, pour numérateur, la somme des deux nombres de la fraction qui l’engendre.
À partir de cet arbre, on peut lister les nombres rationnels en lisant l’arbre ligne horizontale après ligne horizontale, de gauche à droite :
1 / 1, 1 / 2, 2 / 1, 1 / 3, 3 / 2, 2 / 3, 3 / 1, 1 / 4, 4 / 3, 3 / 5, 5 / 1, 1 / 5…
Démontrez que toute fraction qui apparaît dans cette liste est irréductible et que tous les nombres rationnels strictement positifs apparaîtront dans cette liste.
Référence :
Raisonnements divins. Martin Aigner et Günter Ziegler, Springer, 2013.

