Comment découper un rectangle, éventuellement carré, en quatre rectangles dont les diagonales soient toutes des nombres entiers (dans une certaine unité de longueur) ? Dans un tel cas, les dimensions du rectangle initial peuvent-elles être également des nombres entiers (dans la même unité) ?
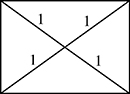
On peut évidemment trouver un rectangle tel qu’un point intérieur soit situé à des distances toutes entières des quatre sommets, mais que les dimensions de ce rectangle ne soient pas entières. Il suffit, pour s’en convaincre, de considérer le rectangle suivant, dont la longueur et la largeur peuvent varier continûment et prendre des valeurs non entières, bien que les quatre distances du centre aux sommets soient toutes égales à une unité.
Voici maintenant une énigme extraite des épreuves du rallye mathématique de Lorraine (2018). Au Mathpays, les quatre villes principales sont situées aux sommets d’un rectangle et se ravitaillent en eau au puits P. Mais quelle distance sépare Mathville du puits ?
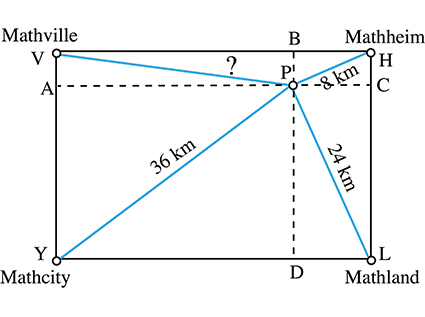
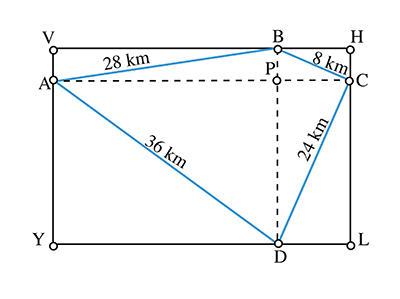
On désigne le puits par P, Mathville par V, Mathheim par H, Mathcity par Y et Mathland par L. La résolution de l’énigme se fait grâce à l’égalité PV2 + PL2 = PY2 + PH2, d’où l’on tire PV = 28 km.
Cette égalité est vraie pour tout point du plan positionné relativement aux sommets d’un rectangle, que ce point soit situé à l’intérieur ou à l’extérieur du rectangle, et sa démonstration ne fait appel qu’au théorème de Pythagore.
Hélas, dans le cas de cette figure, les dimensions des quatre rectangles PAVB, PBHC, PCLD et PDYA ne peuvent pas être toutes entières.
1. Comment le démontrer ?
Les quatre petits rectangles de la figure possèdent chacun deux diagonales égales. On peut donc remplacer respectivement PV, PH, PL et PY par AB, BC, CD et DA.
On obtient ainsi un quadrilatère ABCD inscrit dans un rectangle VHLY. Le premier a ceci de particulier que ses diagonales sont orthogonales : il s’agit d’un quadrilatère orthodiagonal. Ses côtés vérifient l’égalité AB2 + CD2 = BC2 + AD2, qui caractérise les quadrilatères orthodiagonaux.
Le mathématicien indien Brahmagupta (598–670) s’intéressa à ce type de quadrilatère. Il trouva notamment le plus petit exemple de quadrilatère orthodiagonal dont les côtés et les deux diagonales sont tous égaux à des nombres entiers dans une même unité de longueur.
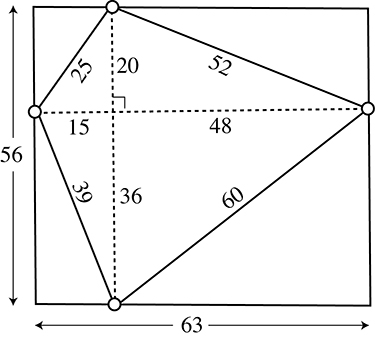
Mais ce quadrilatère possède une autre propriété remarquable : il est inscriptible dans un cercle.
2. Comment le démontrer ?
SOURCES
Perdu dans la forêt. Lucien Pianaro, Jouer Jeux Mathématiques 16, 1995. Pierre est toujours perdu. Lucien Pianaro, Jouer Jeux Mathématiques 17, 1995.

