L’Institut intergalactique, dont le proviseur M. Lambda fait feu de tout bois pour en assurer la promotion, a gagné le privilège d’accueillir une épreuve des JOA (les Jeux olympiques antiques). Point de star squash ou de rallye interplanétaire, on revient ici aux basiques de la Vieille Terre avec un tournoi de tennis où chaque match se joue en trois sets gagnants. En tant que sportif accompli, Alpha a la charge d’apporter une touche locale à la sélection, grâce à un statut d’invité d’honneur (une wild card décrochée par Lambda). Mais il ne se fait guère d’illusions : « Je vais jouer contre Raferak Nadererovic au premier tour, soupire-t-il à l’intention de sa camarade Epsilon. Je n’ai aucune chance de gagner… Remporter ne serait-ce qu’un jeu tiendrait du miracle !
‒ Aucune chance, c’est à prouver ! réagit aussitôt la jeune fille. Gagner un match, c’est gagner trois sets, gagner un set, c’est gagner six jeux, gagner un jeu, c’est gagner quatre points. Et ta probabilité de gagner un point contre Nadererovic n’est pas complètement nulle…
‒ Tu n’as pas tort sur le fond, reconnaît Alpha. D’autant que le comptage des points a été simplifié et qu’il n’y a plus besoin d’avoir deux points d’écart pour gagner un jeu, ni de deux jeux d’écart pour gagner un set.
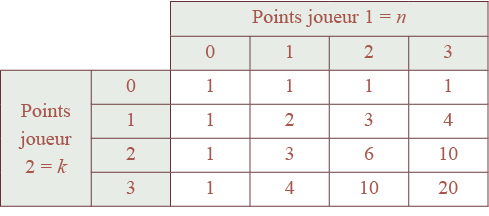
‒ Supposons que tu aies une probabilité p de remporter un point alors que celle de Nadererovic est de q = 1 ‒ p, reprend Epsilon. Et même si ce n’est pas tout à fait vrai, car un point gagné peut t’avoir boosté ou au contraire fatigué et que servir apporte un avantage, supposons également que le résultat lié à chaque point soit indépendant du précédent. On pourrait commencer par faire un tableau comptabilisant les occurrences de tous les scores possibles. Ainsi, si n est le nombre de points du joueur 1 et k le nombre de points du joueur 2, il n’y a qu’une façon d’obtenir un score n à 0, n façons d’obtenir un score n à 1, puis chaque score (n, k) peut être obtenu d’un nombre de façons donné par la somme du nombre de façons d’obtenir (n ‒ 1, k) et le nombre de façons d’obtenir (n, k ‒ 1), seuls états antérieurs possibles. »
Des probabilités pas complètement nulles
« La probabilité que tu gagnes un jeu blanc est de p4, reprend Epsilon, car c’est le produit des probabilités que tu gagnes chaque point. Avec l’aide du tableau, on doit pouvoir trouver la probabilité que tu gagnes un jeu avec les scores 4/1, 4/2 et 4/3. La somme de ces probabilités te donnera celle de remporter un jeu face à Nadererovic. »
Et vous, cher lecteur, sauriez-vous établir cette formule ?
« Si j’estime avoir une chance sur quatre de gagner chaque point, la probabilité de gagner un jeu n’est pas complètement nulle, concède Alpha. Et est-ce que je pourrais espérer gagner un set ?
‒ Il suffit de procéder de la même façon, explique Epsilon, en dénombrant toutes les façons de remporter six jeux et en sommant les probabilités associées. »
Cher lecteur, sauriez-vous calculer cette nouvelle probabilité ?
« Bon, là, ce n’est vraiment pas terrible, soupire Alpha. Et soyons fou, quelles sont mes chances de gagner ce match contre Nadererovic ? »
Cher lecteur, sauriez-vous calculer cette dernière probabilité en supposant qu’Alpha ait une chance sur quatre de gagner chaque point contre son adversaire ?

