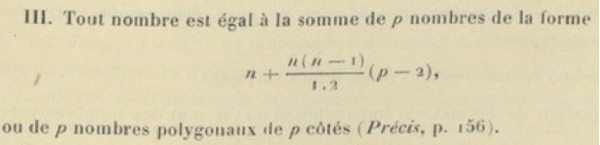
En 1750, Leonhard Euler démontre le théorème dans le cas des nombres pentagonaux. En 1770, Joseph-Louis Lagrange donne une démonstration pour le cas des carrés, qui avait déjà été conjecturée par Claude-Gaspar Bachet de Méziriac en 1621. En 1796, Gauss traite le cas des nombres triangulaires, et précise également le nombre de telles représentations pour chaque entier. Enfin, en 1813, Cauchy vient à bout du cas général.
Dans ces théorèmes, l’expression « au plus » est importante car pour k > 4, lorsqu’on s’aventure vers de grands nombres, le nombre maximum théorique de nombres k-gonaux non nuls devient de moins en moins fréquemment nécessaire. Dans plusieurs cas, ce maximum théorique ne s’impose que pour un nombre fini d’entiers, même si cela n’est parfois encore qu’une conjecture.
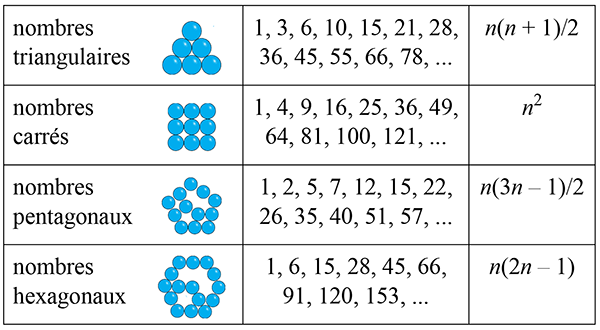
Sommes de nombres triangulaires
Si tout nombre entier est somme d’au plus trois nombres triangulaires, certains entiers non triangulaires peuvent s’écrire comme sommes de seulement deux nombres triangulaires, par exemple 2, 4, 7, 9, 11, 12, 13, 16, 18, 20, 22, contrairement à 5, 8, 14, 17, 19, 23 ou encore 26, qui ne peuvent pas s’écrire comme sommes de moins de trois nombres triangulaires. La clé de la distinction entre ces deux suites, explicitée par Gauss, est la suivante : un nombre n non triangulaire peut s’écrire comme une somme d’exactement deux nombres triangulaires si et seulement si tous les facteurs premiers congrus à 3 modulo 4 du nombre 4n + 1 apparaissent avec un exposant pair.
1. Écrivez 2024 comme une somme de nombres triangulaires comprenant le moins de termes possibles.
Nombres carrés et pentagonaux
Certains nombres ne peuvent pas s’écrire comme sommes de moins de quatre carrés non nuls : 7, 15, 23, 28, 31, 39, 47, 55, 60, ... Gauss a démontré que l’ensemble de ces nombres coïncide avec l’ensemble des nombres de la forme 4a(8k + 7), où a et k sont des entiers naturels. Un autre théorème, dû à Fermat, énonce que tout nombre premier congru à 1 modulo 4 peut s’écrire comme une somme de deux carrés, et ce d’une seule façon. De nombreuses conjectures subsistent sur le nombre de termes nécessaires et le nombre de représentations d’entiers naturels par des sommes de carrés tous distincts, ou deux à deux premiers entre eux, etc.
On ne connait que six entiers qui ne peuvent pas s’écrire comme une somme de moins de cinq nombres pentagonaux. Le plus petit d’entre eux est 9 et le plus grand 89. On a testé les entiers jusqu’à plusieurs millions et on n’en a pas trouvé d’autre.
2. Quels sont les quatre autres entiers connus dont l’écriture en somme de nombres pentagonaux nécessite quatre termes ?
Sommes de nombres hexagonaux
Il n’existe que deux entiers naturels qui nécessitent six termes pour être écrits comme sommes de nombres hexagonaux : 11 et 26. Il n’en existe également qu’un nombre fini qui nécessitent au moins cinq nombres hexagonaux : 5, 10, 11, 20, 25, 26, 38, 39, 54, 65, 70, 114, 130.
Dans ce cas, on sait que la suite est complète. En effet, Legendre à démontré en 1830 que tout nombre entier plus grand que 1791 peut s’écrire comme une somme d’au plus quatre nombres hexagonaux, et les nombres compris entre 130 et 1791 peuvent tous s’écrire comme des sommes d’au plus quatre nombres hexagonaux.
On pense également que le nombre d’entiers naturels dont l’écriture sous la forme de nombres hexagonaux en nécessite au moins quatre est fini, mais on n’en n’a pas la preuve.
Le plus grand entier connu ne pouvant pas s’écrire comme une somme de moins de quatre nombres hexagonaux est le nombre 146 858.
3. Ecrivez 146 858 sous forme d’une somme de nombres hexagonaux.

