En passant du point au segment de droite, nous passons de la dimension 0 à la dimension 1. Pour passer de la dimension 1 à la dimension 2, il faut dupliquer le segment dans une direction autre que celle de ce segment afin d’obtenir un quadrilatère, un carré par exemple. En dupliquant ce carré dans une direction perpendiculaire à son plan, on accède à la troisième dimension, ce qui nous permet de former un solide, un cube par exemple.
En itérant ce procédé à partir d’un cube, nous formons un polytope : l’hypercube de dimension 4, appelé aussi tesseract ou octachore.
Il n’est pas aisé de représenter un tel objet, puisque la quatrième dimension doit être perpendiculaire à chacune des trois premières, ce qui n’est pas possible dans l’espace usuel. Nous devons donc recourir à des projections dans un espace à trois dimensions, que nous représentons dans un espace à deux dimensions, celui de la feuille de papier.
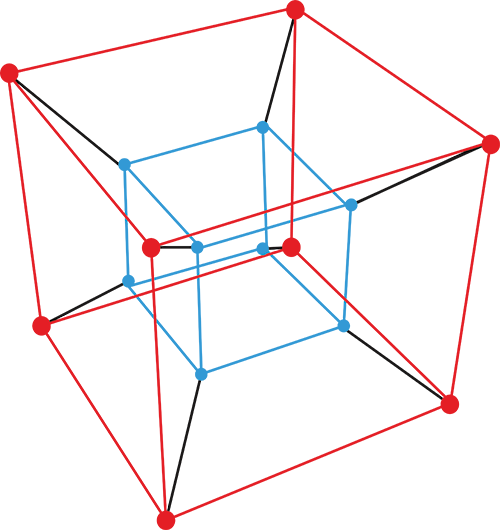
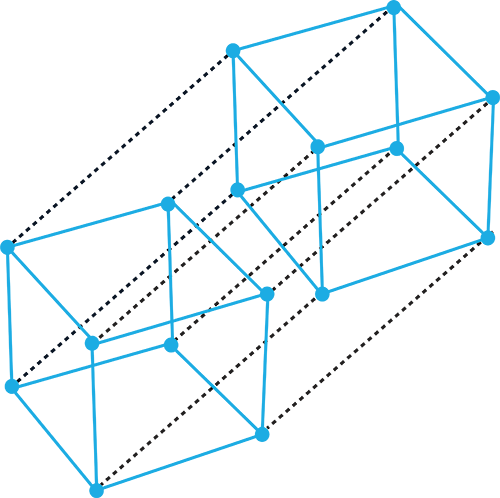
La représentation de gauche est due au mathématicien prussien Victor Schlegel (1843-1905). Celle de droite peut être vue comme le déplacement d’un cube, la quatrième dimension correspondant au temps, une idée imaginée en mécanique par d’Alembert puis par Lagrange.
En théorie des graphes
Les représentations d’un hypercube peuvent être vues comme des graphes, ce qui n’a pas échappé aux théoriciens de cette branche des mathématiques.
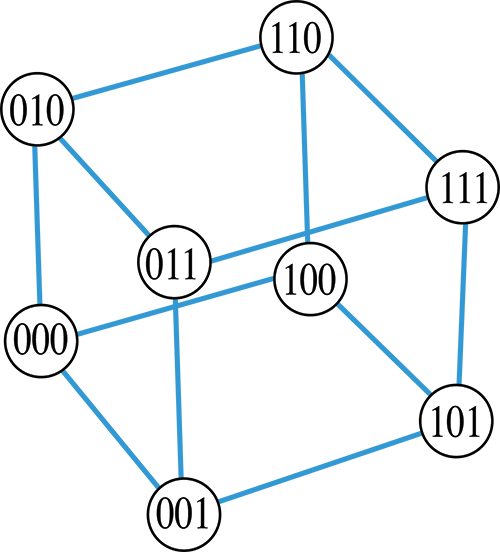
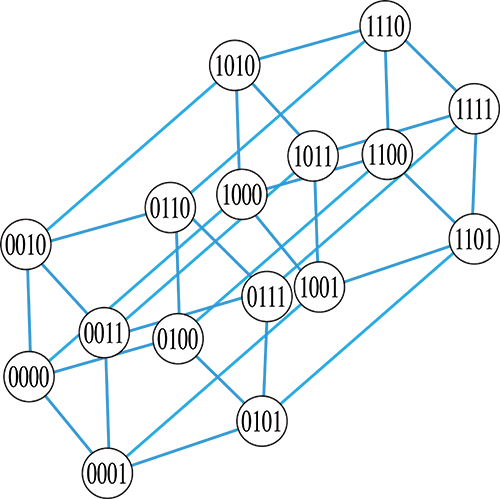
Un étiquetage des sommets peut se faire à l’aide de nombres binaires ayant un nombre de chiffres égal à la dimension. Pour le cube, on donne à un sommet l’étiquette « 000 ». On complète une face avec les étiquettes « 001 », « 010 » et « 011 ». On étiquette ensuite la face opposée avec les mêmes nombres où le premier « 0 » a été remplacé par un « 1 ». Ainsi, sur un même plan, les sommets ont tous un chiffre en commun (même valeur et même position). L’intérêt de cet étiquetage est que chacune des arêtes du graphe relie deux sommets dont l’étiquette diffère d’un seul chiffre. Cette propriété peut s’avérer utile pour trouver des chemins sur un graphe.
1. Combien existe-t-il de cycles (chemins fermés) passant par les huit sommets sur le graphe du cube ?
Magie de l’hypercube
La magie arithmétique, après avoir exploré les figures planes, carrés, cercles, polygones étoilés, s’est ouverte à la dimension 3 avec les cubes magiques. Un météorologue et mathématicien amateur canadien, John R. Hendricks (1929-2007), s’est passionné pour les figures magiques, notamment pour les hypercubes. Il a répertorié les 58 hypercubes magiques normaux (contenant les entiers de 1 à 81) d’ordre 3.
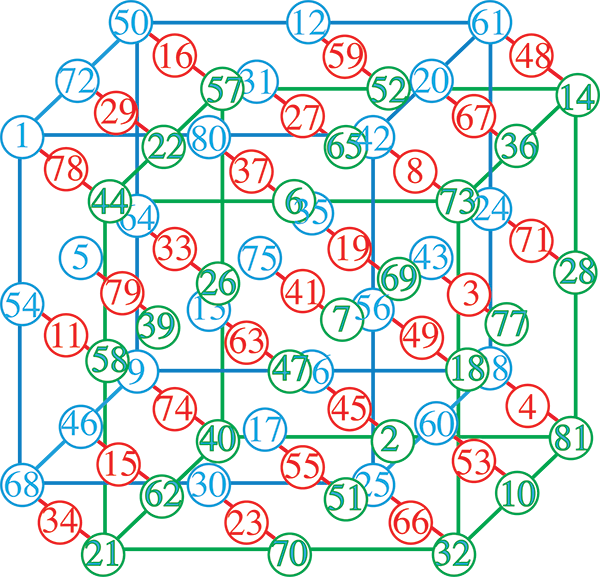
Dans cet hypercube, les 27 rangées dans chacune des quatre directions de l’hyperespace présentent une somme égale à 123 ; par exemple :
50 + 12 + 61 = 50 + 72 + 1 = 50 + 64 + 9 = 50 + 16 + 57 = 123.
Il en est de même pour chacune des 8 diagonales des cubes comme 1 – 41 – 81.
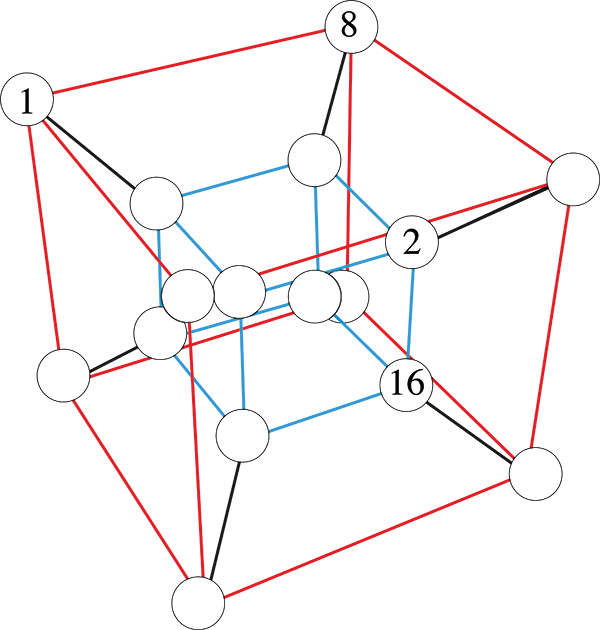
Une autre possibilité, plus simple, consiste à placer les nombres de 1 à 16 sur les 16 sommets d’un hypercube d’ordre 2, de telle sorte que la somme des nombres sur chacune de ses 24 faces soit toujours la même. Cet hypercube peut se construire à partir des nombres d’un carré magique 4 × 4, en réarrangeant astucieusement ces nombres.
2. Placez les nombres de 1 à 16 (sauf 1, 2, 8 et 16 déjà placés) dans les cases vides du diagramme de cet hypercube afin que la somme des nombres appartenant à une même face soit toujours la même.