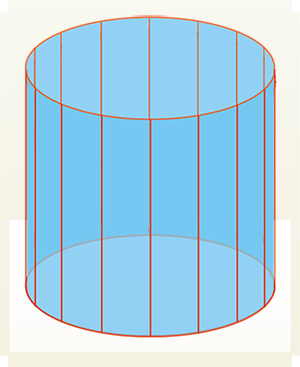
Imaginez que l'on cherche à construire une surface… à partir de droites. La première surface réglée qui vienne à l'esprit quand on veut échapper au plan est le cylindre, une sorte de plan enroulé. On peut le construire également à partir de deux roues montées sur un même axe métallique, en tendant des élastiques entre elles.
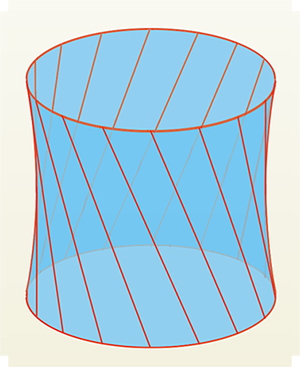Il suffit de tourner l'une des roues, celle du dessus par exemple, pour obtenir un objet plus surprenant. Les élastiques se déplacent et une nouvelle surface apparaît. Elle porte le nom compliqué d'hyperboloïde de révolution à une nappe. Son équation dans un repère orthonormé bien choisi est de la forme x2 + y2 – k2 z2 = 1 où k > 0 (l'axe (Oz) est donc l'axe des roues et l'unité a été choisie pour simplifier l'équation).
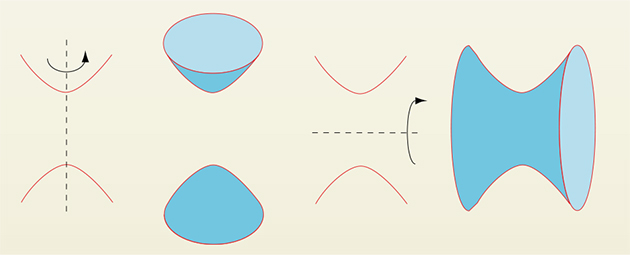
Pourquoi un tel nom ? Tout simplement parce qu'on l'obtient également en faisant tourner une hyperbole autour de l'un de ses axes. Si on fait tourner la même hyperbole autour de son autre axe, on obtient une surface en deux parties, ou deux nappes. Pour distinguer ces deux surfaces très différentes, on précise toujours le nombre de nappes.
