Tangente Mag

C'est un plaisir de l'oeil de voir certaines figures géométriques présentant de nombreuses droites habilement placées et le long desquelles s'enlace une jolie courbe qui semble effleurer chacune d'entre elles. Quelle théorie mathématique se dissimule derrière ? C'est celle des enveloppes de droites.

Entre 1620 et 1670, les plus prestigieux mathématiciens, comme René Descartes, Pierre de Fermat ou John Wallis, ont cherché à établir une méthode pour déterminer l’équation de la tangente à une courbe. L’introduction du calcul différentiel par Isaac Newton et Gottfried Wilhelm Leibniz à la fin du XVII ^e siècle a résolu ce problème de manière magistrale. On s’est aussitôt posé le problème inverse : étant donnée une famille de droites, peut-on trouver une courbe qui les admette toutes pour tangente ?

De la géométrie à l’analyse

Prenons un exemple géométrique simple. Considérons des axes rectangulaires (Ox) et (Oy)

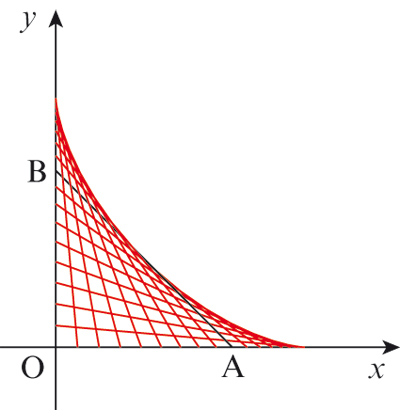
et faisons glisser un segment [AB] de longueur a tel que A soit sur l’axe (Ox) et B sur (Oy) :

on voit apparaître une courbe dont toutes les droites, obtenues en prolongeant ces segments, sont les tangentes.

Ces droites ont pour équation x cos t + y sin t = 5 sin 2 t.

Après résolution (voir FOCUS), on obtient une astroïde, d’équation paramétrique t ? (cos³t, sin³t) ou d’équation cartésienne x ²^/3 + y ²^/3 = 1. On peut la visualiser en prenant une réglette d’une longueur donnée, en la plaçant un grand nombre de fois avec chacune de ses extrémités positionnées sur chacun de deux axes orthogonaux, et en traçant les droites ... Lire la suite

Comment rechercher l'enveloppe

On se place dans un plan euclidien muni d’un repère orthonormé et on se donne une famille de droites indexées par un paramètre, noté t. Plus précisément, la droite D_t a pour équation a (t) x + b (t) y + c (t) = 0 où a, b et c sont des fonctions dérivables et de dérivées continues sur un intervalle I des nombres réels.

S’il existe une courbe paramétrée telle qu’en tout t de I la tangente à cette courbe est la droite D_t, alors celle-ci est paramétrée par t ? (x(t), y(t)), où les fonctions x et y sont solutions du système suivant :

$\left\{ \begin{array}{l l} a(t)x + b(t) y +c(t)=0,\\[2mm] a'(t)x + b'(t) y +c'(t)=0.\\ \end{array} \right.$

La première équation exprime le fait que le point courant M(t) est sur la courbe. En la dérivant, on obtient a’ (t) x + b’ (t) y + c’ (t) + a (t) x’ (t) + b (t) y’ (t) + c(t) = 0. Or la normale (droite orthogonale à la tangente) au point de paramètre t est dirigée par le vecteur (a(t), b (t)), qui est orthogonal au vecteur tangent dirigé par ( x’ (t), y’ (t)). Leur produit scalaire est donc nul, ce qui annule le terme a (t) x + b (t) y ; on en déduit la seconde équation.

Prenons pour exemple les droites D_t : x – y cos t – sin t = 0.

Le système à résoudre est alors :

$\left\{ \begin{array}{l l} x(t)- y(t) \cos t-\sin t=0,\\[2mm] y(t)\sin t - \cos t =0.\\ \end{array} \right.$

On en déduit, si t n’est pas nul, que y(t) = cos(t) / sin(t), puis que x (t) = 1/ sin(t) ; on obtient enfin l’hyperbole équilatère d’équation x ² – y ² = 1.

Construction simple d’une famille de droites.

Réunion de famille

Bertrand Hauchecorne

dossier : Enveloppes de familles de droites

Tangente 187 : Enveloppes de familles de droites

De la géométrie à l’analyse