Cette très jolie propriété géométrique était connue des élèves de seconde C dans les années 1970, même si peu savaient la démontrer.

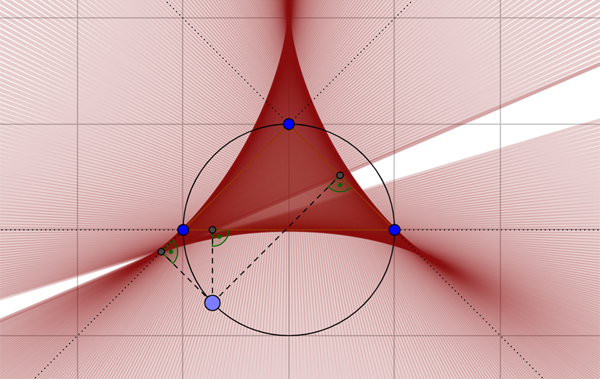
Soit ABC un triangle et M un point du plan. Les projections de M sur les trois côtés du triangle sont alignées si, et seulement si, le point M appartient au cercle circonscrit au triangle ABC. Si c’est le cas, la droite qui joint les trois projections est appelée droite de Simson du point M.
.jpg)
Une propriété encore plus jolie est le théorème de Steiner : quand M décrit le cercle circonscrit, la droite de Simpson de M enveloppe une hypocycloïde à trois points de rebroussement. Cette courbe est celle que décrit un point d’un cercle de rayon R roulant sans glisser à l’intérieur d’un cercle de rayon 3R.