
Que faire face à un problème de construction ? Le bon sens veut que l’on commence à esquisser à main levée la figure souhaitée, puis que l’on recherche sur le tracé obtenu certaines caractéristiques géométriques des éléments présents, qui fourniront un protocole de construction. La dernière étape sera celle de la validation du résultat graphique ainsi construit.
Analyse et synthèse
La démarche a été codifiée au fil des âges par les géomètres et elle a un nom : analyse et synthèse. Elle s’applique à tous les domaines des mathématiques, mais c’est ici dans le domaine géométrique que nous allons la considérer. Laissons le mathématicien français François Viète (1540–1603), qui en son temps a su transformer l’algèbre (voir Tangente 194, 2020), évoquer son évolution historique dans son ouvrage Isagoge in artem analyticem : « Il est en mathématiques une méthode pour la recherche de la vérité que Platon passe pour avoir inventée, que Théon a nommée analyse et qu’il a définie ainsi. Regarder la chose cherchée comme si elle était donnée, et marcher de conséquences en conséquences, jusqu’à ce que l’on reconnaisse comme vraie la chose cherchée. Au contraire la synthèse se définit : partir d’une chose donnée, pour arriver de conséquences en conséquences à trouver la chose cherchée. »
Le philosophe allemand Emmanuel Kant (1724–1804) ne dit pas autre chose lorsqu’il parle de méthode « régressive » pour l’analyse et de méthode « progressive » pour la synthèse.
La résolution d’un problème de construction géométrique va donc s’opérer en deux temps :
• Première phase : l’analyse. C’est dire que l’on suppose le problème résolu (exactement ce qu’on a fait en traçant le croquis à main levée), et on observe la construction déjà faite, du moins approximativement, comme si c’était « la » solution. C’est ce que le mathématicien spécialiste de didactique Georges Glaeser (1918–2002) appelait « localiser les notions essentielles, distinguer ce que l’on sait déjà de ce que l’on aimerait savoir ». On tente d’y repérer comment les éléments géométriques que l’on doit construire sont liés aux éléments déjà donnés, et aussi comment ils sont liés entre eux. Là, on peut chercher à ramener le problème à la recherche de points déterminants dont la connaissance permettra d’achever la figure demandée. On pourra les identifier comme intersections de droites, cercles, courbes…, ou leur reconnaître des propriétés qui aideront à achever la figure.
Cette phase d’analyse amène finalement à déterminer des conditions nécessaires à la réalisation de la construction finale.
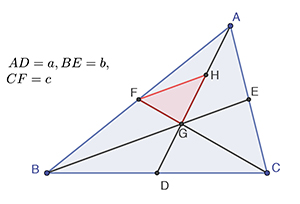
Triangle dont on ne connaît que les longueurs des médianes.
C’est ainsi que s’il est demandé de reconstituer un triangle dont on connaît les longueurs a, b, c des trois médianes. En supposant le problème résolu, on peut par exemple remarquer, si H est le milieu du segment [AG], que le triangle FGH a ses côtés égaux au tiers de ceux du triangle ABC que l’on cherche à construire. C’est cette particularité que l’on va exploiter pour achever la construction du triangle ABC : on sait en effet, à partir du segment [AD], de longueur A, et le point G au tiers de ce segment à partir de D, tracer le triangle FGH dont les côtés ont pour longueurs a / 3, b / 3 et c / 3, ce qui permettra de placer correctement les points C et B. Ici, c’est le point H qui a été déterminant dans la suite de la construction.
• Deuxième phase : la synthèse. C’est en quelque sorte la « réciproque » de la phase précédente. Dans un premier temps, à la lumière des renseignements tirés de l’analyse, on va réaliser la construction à effectuer en justifiant ses étapes l’une après l’autre. Dans un deuxième temps, on déterminera la limite ou les impossibilités éventuelles de cette construction, ce qui pourra donner lieu à l’ouverture d’une discussion : y a-t-il des cas où la construction n’est pas possible ? peut-il exister plusieurs solutions ?
Mise en pratique
Si l’on demande, par exemple, de construire un cercle tangent à une droite donnée d et passant par deux points A et B donnés, si A et B sont de part et d’autre de la droite d, il n’y aura pas de solution. La synthèse conduit par ailleurs à une discussion sur le nombre de solutions dans les autres cas : si A est sur d et B à l’extérieur, il y aura une seule solution, le cercle centré à l’intersection de la perpendiculaire en A à d et de la médiatrice de [AB] ; si la droite (AB) est parallèle à d, il y aura là aussi une solution unique, le point de contact étant comme précédemment l’intersection de d et de la médiatrice de [AB]. Dans tous les autres cas, on trouvera deux cercles-solutions et on les déterminera en construisant d’abord leurs points de contact avec d.
Une construction due à Wallis
On doit au mathématicien britannique John Wallis (1616–1703) un tracé inventif comme solution au problème de construire un cercle tangent à une droite donnée d et passant par deux points donnés A et B. Supposons, pour que ce problème ait une solution, que les deux points A et B sont situés du même côté de d et non sur d et que la droite d n’est pas parallèle à (AB) ; dans ces cas particuliers, la solution est unique. La droite (AB), dans le cas considéré, coupe d au point I et Wallis va utiliser la puissance de I par rapport au cercle cherché.
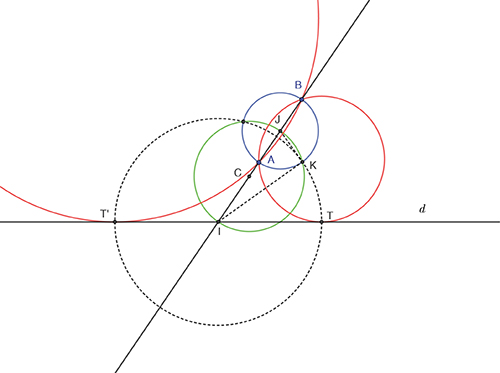
Cercle passant par deux points et tangent à une droite donnée.
Analyse : Si un tel cercle existe, T étant le point de contact de ce cercle avec d, IA × IB = IT2 (on dit que IT est moyenne proportionnelle entre IA et IB). C’est sur cette valeur que se focalisera l’intérêt de Wallis : il va construire un point K tel que IT = IK.
Synthèse :
Réalisation de la construction : cela commence par la recherche d’un point K convenable. Wallis le situera à l’intersection des cercles de diamètre [AB] (bleu) et du cercle de diamètre [IJ] (vert). En effet, comme K est sur le cercle de diamètre [IJ], (JK) est perpendiculaire à (KI). Cette dernière droite est tangente en K au cercle bleu, donc IK2 = IA × IB.
Discussion : on construit un point T sur d tel que IT = IK et on conclut aussitôt qu’il existe un autre point T’, symétrique de T par rapport à I, tel que IT’ = IT. Le problème proposé a donc deux solutions : les cercles circonscrits aux triangles ABT et ABT’.
La méthode par analyse et synthèse, si elle s’applique dans de nombreux domaines des mathématiques, est spécialement bien adaptée aux problèmes de construction.
Le carré inscrit
De nombreuses constructions classiques permettent de mettre en évidence la méthode d’analyse et synthèse. « Inscrire un carré dans un triangle » est l’une d’elles ; il s’agit, étant donné un triangle quelconque ABC, de construire un carré dont deux sommets se trouvent par exemple sur le côté [BC], les deux autres étant, l’un sur [AB], l’autre sur [AC].
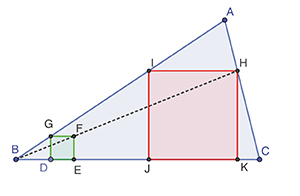
Analysons le problème : ce que l’on sait faire, c’est construire un « petit » carré (en vert) dont deux sommets, D et E, sont sur [BC], le troisième, G, sur [AB], mais le quatrième, F, n’est a priori pas sur [AC]. Qu’à cela ne tienne : une homothétie h de centre B va l’y amener, celle qui transforme F en un point H de [AC]. Par h, la droite (AB), qui passe par le centre d’homothétie, est sa propre image, et la droite (GK) aura pour image sa parallèle passant par H. Ces deux images se couperont en I, sur [AB]. Et voilà le côté de notre carré !
Il ne faut pas oublier de faire la synthèse : le fruit de l’analyse nous donne donc, à partir du carré intermédiaire DEFG, le segment [IH], H étant obtenu comme étant sur [AC], et image de F par l’homothétie h de centre B. Le point I est alors l’image de G dans cette même homothétie. On construit en plus les deux points du côté [BC], J, image de D, et K, image de E, et on est assuré que le quadrilatère IJKL, image d’un carré par homothétie, est bien lui aussi un carré.
Une question se pose maintenant : une telle construction est-elle toujours possible ?
La réponse est « oui » dans le cas d’un triangle ABC acutangle. Si l’un des angles de ce triangle est obtus, en B par exemple, on choisira une homothétie h de centre C (forcément aigu) et le carré IJKL aura ses sommets, non pas sur les segments que définissent les côtés, mais sur les droites qui les prolongent.
