La distance usuelle, celle de la ligne droite comme plus court chemin entre deux points M1 et M2 du plan, est la distance euclidienne ; on la notera ici d (M1, M2). Mais bien d’autres distances peuvent être définies. Dans notre plan habituel muni d’un repère orthonormé, on va associer à chaque point ses coordonnées, fournies par un couple de réels (son abscisse et son ordonnée). À chaque distance considérée sont associées des « boules » : une boule de centre M0 et de rayon r est l’ensemble des points dont la distance à M0 est inférieure ou égale à r. Ce terme générique est employé dans tous les espaces métriques. En l’occurrence ici, les boules sont planes : par exemple, les boules associées à la distance euclidienne sont les disques.
À base d’horizontales et de verticales
Commençons par une distance liée à une norme, la 1-norme. Si M1(x1, y1) et M2(x2, y2) sont deux points du plan, la distance d1 entre ces deux points est définie par :
d1(M1, M2) = | x2 – x1| + | y2 – y1|.
On montre aisément que d1 vérifie les trois conditions requises pour être une distance.
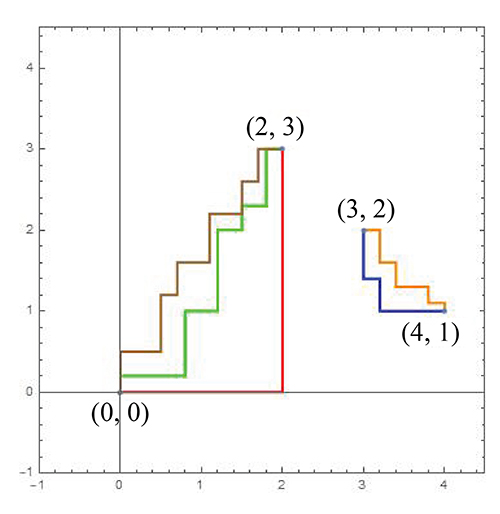
Pour avoir le chemin le plus court d’un point à un autre avec d1, il faut suivre uniquement les ... Lire la suite
