
Des arbres pour les notions probabilistes…
Un jeu forain consiste à choisir au hasard une boîte parmi trois d’apparence identique. Elles contiennent respectivement trois, deux et un seul jetons, tous argentés sauf un seul par boîte qui est doré.
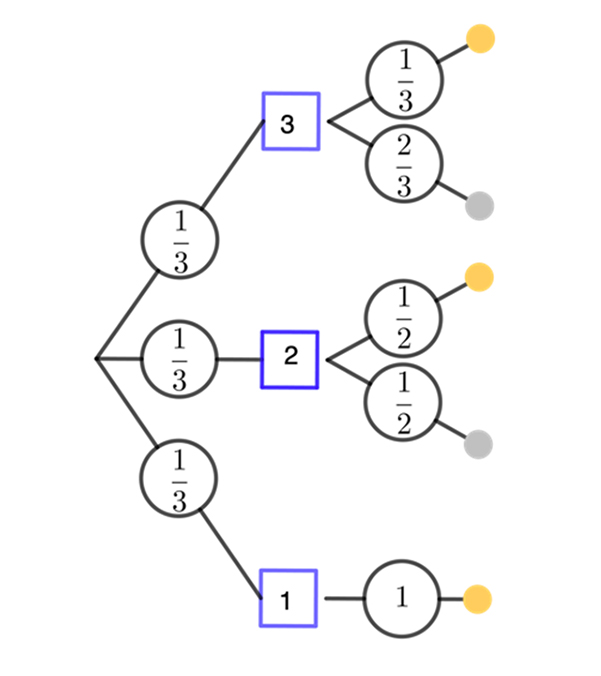
Arbre à deux niveaux représentant les éventualités possibles (éventualité de boîte en premier niveau, suivie de celle de couleur de jeton). Du tirage dans la boîte contenant trois jetons, par exemple, on observe l’éventualité « jeton doré » avec la probabilité 1/3, et l’éventualité « jeton argenté » avec la probabilité 2/3.
La mise en œuvre de l’arbre probabilisé met en évidence, en la représentant, la notion de probabilité conditionnelle et facilite l’appréhension de sa définition. Pour deux évènements A et B, on a P(A et B) = P(A)×PA(B) où PA(B) est la probabilité de B sachant A. Sur l’exemple, la probabilité de l’éventualité « boîte à trois jetons et jeton doré » vaut bien (1/3)×(1/3).
Si l’on souhaite calculer la probabilité d’obtenir un jeton doré, on aura
P(« jeton doré ») =
Dès lors on peut affronter une question comme : sachant que le jeton est doré, quelle est la probabilité que ce soit celui de la boîte contenant deux jetons ? On peut alors ébaucher un nouvel arbre, inversé par rapport au précédent.
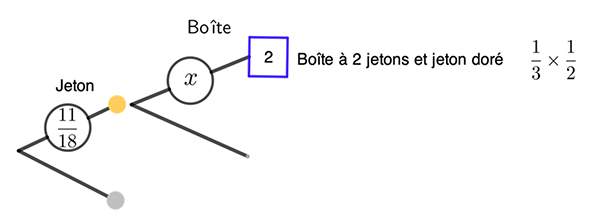
La probabilité conditionnelle x cherchée est alors soit 3/11.
En la représentant, l’arbre probabilisé participe à mettre en place la formule de Bayes. C’est un instrument pédagogique.
Par exemple ici, avec deux évènements A et B, la formule serait simplement où
désigne l’évènement contraire de A.
Références
• Des statistiques aux probabilités. Bernard Parzysz, Repères IREM 10, janvier 1993.
• Les graphes. Bibliothèque Tangente 54, 2015.
… et pour dénombrer
La représentation par arbre de situations d’épreuves répétées ou successives est un moyen éclairant la caractéristique multiplicative attachée au dénombrement de leurs issues. Prenez le clown Marcello. Il a trois gibus de couleur différente, cinq vestons eux aussi de couleur différente, un pantalon uni, un autre rayé, et un short, une paire de souliers (bien trop grands). Combien de tenues de spectacle cela lui fait-il, s’il néglige les assortiments ?
On dessine un arbre, de gauche à droite : un niveau pour le gibus (trois rameaux), un pour les vestons (cinq rameaux pour chaque extrémité précédente), un pour les pantalons. À l’évidence, le nombre de tenues est 3×5×3, soit 45.
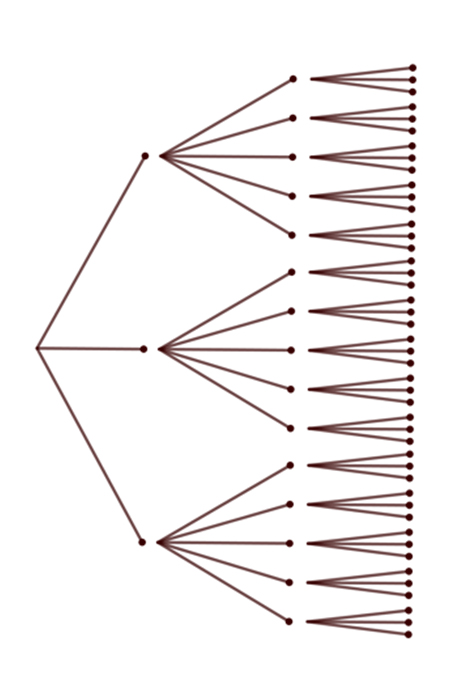
Des épreuves à répétition
Lors de la répétition d’une même épreuve à deux issues (pile ou face), l’évolution des possibilités est figurée par un arbre ayant, à chaque répétition, deux rameaux vers chaque résultat : P pour pile (vers le haut), F pour face (vers le bas). Avec deux épreuves, on perçoit qu’il y a exactement 2 × 2 = 4 issues. Avec n épreuves, il y en a 2 n.
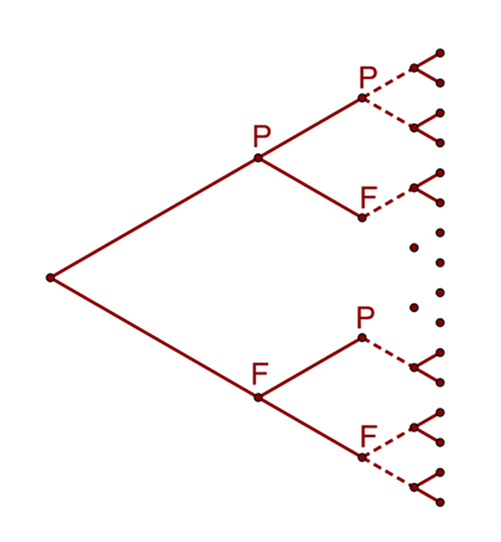
Parmi ces issues, observons le nombre de celles qui comportent un nombre fixé de piles. Pour deux épreuves, on pourra avoir soit deux P, soit un seul P, soit deux F, avec une double possibilité de réalisation du cas intermédiaire.
Dans la répétition de n épreuves, le nombre d’issues (de chemins sur l’arbre) comportant un nombre de P valant k est égal à k variant de 0 à n ; c’est le nombre de chemins ayant k rameaux « montants ». Comme le nombre total d’issues est 2 n et est aussi la somme des
on a nécessairement
De même, par symétrie de l’arbre.
Références
• Dossier « Les paris ». Tangente 136, 2010.
• Dossier « Les mathématiques des paris ». Tangente 175, 2017.
• Dossier « Le triangle de Pascal ». Tangente 176, 2017.
