
Si l’on suppose, comme dans cet article, que les fonctions réelles sont indéfiniment dérivables, alors leurs développements limités ne sont pas… limités, puisque précisément on peut les effectuer à tout ordre (il serait de fait préférable de les nommer « développements polynomiaux »). En tout point x0, on peut donc écrire
f (x0 + u) = a + bu + cu 2 + du 3 + o(u 3 ), sachant que a = f (x0 ), b = f ′(x0 ), c = f ′ ′ (x0 ) / 2
et d = f ′ ′ ′ (x0 ) / 6 ; et l’on pourrait continuer plus loin.
Les deux premiers termes indiquent que la droite d’équation y = a + b (x ‒ x0) est tangente à la courbe d’équation y = f (x).
Si le coefficient c n’est pas nul, on dit que le point est ordinaire et la courbe tourne sa concavité « vers le haut » s’il est positif, « vers le bas » sinon.
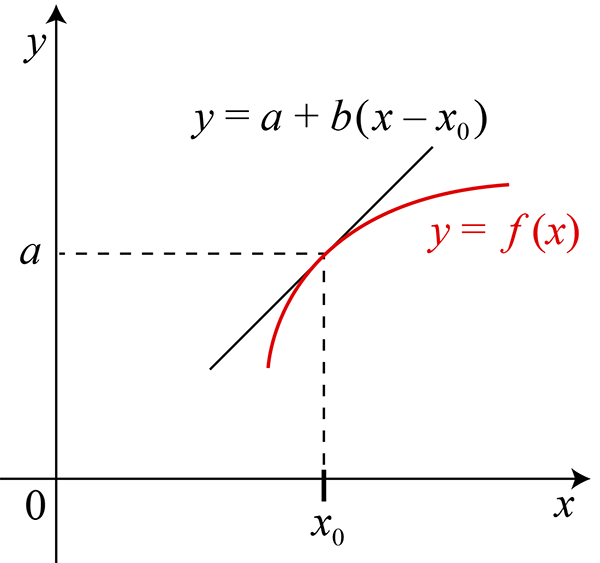
Exemple de point ordinaire avec c < 0.
Si c est nul et d non nul, on dit qu’il y a pointd’inflexion et la courbe traverse sa tangente en arrivant « par au-dessus » si d est positif, « par au-dessous » sinon.

