Un cadeau bien enrubanné

Même les plus jeunes savent reconnaître un multiple de 9 sans se perdre dans de longues divisions (et sans calculatrice) ; il suffit d’additionner les chiffres de l’entier considéré, quitte à recommencer plusieurs fois. Tout multiple de 9 est en effet composé de chiffres dont la somme est elle-même un multiple de 9. Mais qu’en est-il quand on s’intéresse à un autre diviseur potentiel ? Existe-t-il une méthode aussi simple que l’addition des chiffres pour répondre ? Blaise Pascal s’est penché sur la question et en a tiré un petit traité d’une dizaine de pages écrit en latin, De numeris multipicibus, et ne contenant qu’une unique proposition illustrée de nombreux exemples. Le texte a été mentionné en 1654 mais n’a été publié qu’à titre posthume en 1665, à la suite du Traité du triangle arithmétique, dont il est totalement indépendant.
 

Le ruban du maître

Suivons la petite recette exposée par le savant clermontois. Avant de recueillir les fruits de cette pépite arithmétique, il faut construire le ruban qui emballe le cadeau. Quel est donc ce « ruban de Pascal » ?

Notons A le diviseur qui nous intéresse. On commence par un simple tableau à deux lignes :

La valeur du nombre B s’obtient comme suit. Multipliez par 10 la valeur située immédiatement à sa droite, ce qui donne 10, et retranchez autant de fois que possible le diviseur A ; la valeur de B est le reste obtenu.

Recommencez ainsi pour le nombre C : il s’agit du reste obtenu en retranchant autant de fois que possible le diviseur A au produit 10B.

Le nombre D est le reste obtenu en retranchant autant de fois que possible le diviseur A au produit 10C. Et ainsi de suite. La première ligne indique seulement le rang, de droite à gauche, des résultats et n’intervient pas dans les calculs.

Si vous êtes un peu perdu, pas de panique, regardez sur un exemple, cela vaut le coup de s’accrocher. Pascal suggère comme premier cas particulier de prendre l’entier 7 comme diviseur. 

On a B = 10 – 7 = 3.

Multiplions maintenant B par 10, ce qui donne 30. On peut en retrancher quatre fois 7 (soit 28) et il reste C = 2.

Multiplions maintenant C par 10, ce qui donne 20. On peut en retrancher deux fois 7 (soit 14) et il reste D = 6.

Multiplions maintenant D par 10, ce qui donne 60. On peut en retrancher huit fois 7 (soit 56) et il reste E = 4.

Multiplions maintenant E par 10, ce qui donne 40. On peut en retrancher cinq fois 7 (soit 35) et il reste 5.

Assurez-vous que vous trouvez ensuite F = 1.
Inutile de poursuivre, le mécanisme fait que les restes obtenus vont se répéter. Voici donc notre ruban :

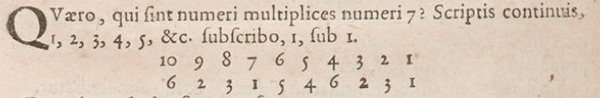
Une mise en œuvre enfantine

Qu’allons-nous faire de ce joli ruban ? Pour garder les notations de Pascal, prenons un nombre à quatre chiffres dont l’écriture décimale est TVNM. 

Par exemple, pour l’entier 1623, on a T = 1, V = 6, N = 2 et M = 3. Écrivons notre nombre sous notre ruban et multiplions terme à terme.

On obtient alors D×T + C×V + B×N + 1×M. L’entier TVNM est un multiple de A si, et seulement si, cette somme l’est aussi.

Reprenons notre ruban de divisibilité par 7. À titre d’exemple, Blaise Pascal se demande si le nombre 287 542 178 est un multiple de 7. À l’aide du ruban, on obtient le tableau suivant.

On calcule la somme 2×2 + 3×8 + 1×7 + 5×5 + 4×4 + 6×2 + 2×1 + 3×7 + 1×8, ce qui donne 119.

Si 119 est divisible par 7, alors 287 542 178 l’est aussi.

Vous ne savez pas si 119 est multiple de 7 ? Eh bien appliquez à nouveau la même méthode ! Le ruban donne cette fois :

La somme vaut 2×1 + 3×1 + 1×9, soit 14. Cette fois-ci, c’est sûr, 14 est un multiple de 7, donc 119 aussi, et 287 542 178 également. Pascal s’amuse, « par curiosité plutôt que par nécessité », à traiter le cas de 14 comme les précédents. La somme à calculer vaut alors 3×1 + 1×4, soit 7.

Reprenons l’exemple proposé en guise de défi au début de cet article : le nombre 19 061 623 est-il divisible par 37 ? Déjà, assurez-vous que le ruban associé à 37 est le suivant :

Appliquons notre ruban à l’entier choisi (clin d’œil à la date de naissance de Pascal) :

Un calcul faisable de tête vous donne une somme égale à 259.

Appliquons encore une fois le ruban :

Cette fois-ci, la somme vaut 111. Vous pouvez encore appliquer le critère de divisibilité si vous n’avez pas remarqué que 111 est le triple de 37. Voilà qui est tout de même plus efficace (et amusant) qu’une division fastidieuse !

La preuve par neuf… ou plus

En quoi tout ceci est-il une généralisation du fameux critère de divisibilité par 9 ? Eh bien, regardez le ruban obtenu pour chercher les multiples de 9 : on retrouve bien la méthode connue depuis la nuit des temps !

Pascal s’étonne que personne à sa connaissance n’ait tenté de généraliser avant lui le fameux critère de divisibilité par 9. Et il s’étonne également que personne n’en ait donné de démonstration. Lui-même prend la peine de justifier sa méthode ; voyons comment il s’y prend.

Le cas des nombres à un seul chiffre est trivial. Pascal passe donc sans délai au cas d’un nombre a à deux chiffres, dont il note NM l’écriture décimale. Le but est donc d’établir que, pour que a = 10N + M soit divisible par A, il faut et il suffit que B×N + M le soit. Par construction du ruban, B est le reste dans la division de 10 par A. Ainsi, 10 – B est divisible par A. En multipliant le tout par N, 10N – B×N est aussi divisible par A. Or a est égal à (10N – B×N) + (B×N + M). Ceci implique bien que a est un multiple de A si, et seulement si, B×N + M en est un aussi.

Qu’en est-il des nombres à trois chiffres ? Supposons donc que l’écriture décimale de a soit maintenant VNM, c’est-à-dire que a = 100V + 10N + M. Le but est d’établir que, pour que a soit un multiple de A, il faut et il suffit que C×V + B×N + M le soit aussi. On a déjà vu que 10 – B est un multiple de A, et donc, en multipliant par 10V, on en déduit que 100V – 10B×V est un multiple de A aussi. Par ailleurs, C est le reste dans la division par A de 10B, donc 10B – C est divisible par A et, en multipliant par V, on en déduit que 10B×V – C×V est divisible par A aussi. On a déjà vu, dans le cas de la démonstration pour les nombres à deux chiffres, que 10N – B×N est aussi un multiple de A. En additionnant le tout, on en déduit que (100V – 10B×V) + (10B×V – C×V) + (10N – B×N) = 100V + 10N – C×V – B×N est un multiple de A. Il ne reste plus qu’à remarquer que a est la somme de 100V + 10N – C×V – B×N et C×V + B×N + M pour conclure !

Pascal se contente ensuite de signaler que la démonstration serait la même si le nombre donné se composait de plus de trois chiffres. Cela pourrait laisser certains lecteurs d’aujourd’hui sur leur faim… mais il ne faut pas oublier que le langage des congruences, parfaitement adapté à la situation, n’apparaîtra que cent cinquante ans plus tard !

Un critère de base

On pourrait penser que le court traité de Pascal, qui ne contient pas d’autre propriété que celle exposée ici, ne se limite qu’à une simple amusette anecdotique. Ce serait faire l’impasse sur certaines remarques de l’auteur qui montrent à quel point ses pensées sont en fait novatrices, voire avant-gardistes. Dès la première page, Pascal indique que cette méthode des rubans s’applique non seulement à notre système de numération décimal, mais encore à tout système de numération ayant pour base le nombre que l’on voudra. En plus d’avoir conscience de l’existence de différents systèmes de numération, Pascal signale que les autres systèmes de numération sont tout aussi légitimes que notre base 10, « système qui repose non sur une nécessité naturelle, comme le pense le vulgaire, mais sur une convention, d’ailleurs assez malheureuse » ! Il faudra attendre encore quelques années avant de lire à nouveau dans la littérature scientifique des réflexions aussi lucides sur le sujet.

À titre d’exemple, Pascal suggère de s’intéresser au système duodécimal, c’est-à-dire à la base 12, « système fort commode sans doute ». Pour écrire les nombres en base 12, il faut utiliser « deux figures nouvelles pour désigner, l’une le nombre 10, l’autre le nombre 11 ». Prenons A pour symboliser le 10 et B pour le 11. Le nombre qui s’écrit B33 en base 12 (et que l’on pourra aussi noter B33 ¹² pour éviter toute ambiguïté) est ainsi égal, en base 10, à 11×12² + 3×12 + 3, soit 1 623.

Pour reconnaître les multiples de 9, on construit un nouveau ruban, mais en prenant soin de changer les multiplications par 10 par des multiplications par 12. On inscrit 1 sous le 1.

Pour le deuxième nombre, on multiplie donc 1 par 10 ¹², soit 12 et on retranche une fois 9, ce qui donne pour reste 3.

À l’étape suivante, on multiplie 3 par 10 ¹², ce qui donne 30 ¹², ou encore « trois fois douze », soit 36. On peut retrancher 4 fois 9 et il reste 0.

Finalement, le ruban est assez simple :

On en conclut le critère de divisibilité suivant relatif au système duodécimal : tous les nombres pour lesquels la somme du dernier chiffre et du triple de l’avant dernier sont multiples de 9 sont eux-mêmes des multiples de 9.

L’auteur signale également que, toujours dans le système duodécimal, tous les nombres dont la somme des chiffres est un multiple de 11 sont eux-mêmes divisibles par 11.

Laissons le mot de la fin à Blaise Pascal lui-même, qui achève son traité par ces mots : « Si j’ai touché ce sujet c’est parce que je cédais volontiers à l’attrait de la nouveauté ; maintenant je m’arrête de peur de fatiguer le lecteur en entrant dans trop de détails. »