
L’un des plus célèbres problèmes de coloriage porte sur le « nombre chromatique du plan ». Qu’est-ce donc ? Le but est d’attribuer une couleur à chaque point du plan de façon que deux points distants d’une unité soient toujours de couleurs différentes. Évidemment, le but du jeu est d’utiliser le moins de couleurs possible, et c’est ce nombre minimal que l’on appelle nombre chromatique du plan, noté χ (ℝ2).
L’examen d’un simple triangle équilatéral permet de se convaincre que χ (ℝ2) ≥ 3. En 1961, le mathématicien canadien Leo Moser (1921‒1970) a proposé un graphe, parfois baptisé broche ou fuseau de Moser, qui permet de constater que χ (ℝ2) ≥ 4. Il a été rapidement établi que χ (ℝ2) ≤ 7. mais il aura fallu ensuite attendre 2018 pour que l’encadrement soit amélioré ; la question reste aujourd’hui ouverte (voir encadré).
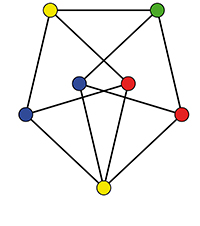
Le fuseau de Moser.
Avec une seule couleur !
Si vous n’avez pas de boîte de crayons de couleur sous la main et seulement un stylo noir, rien ne vous empêche de vous confronter à de belles questions de coloriage pour autant. Dans les années 1960, Leo Moser avait en effet proposé un autre problème moins connu mais tout aussi amusant : quelle proportion maximale du plan peut-on colorer de manière que deux points coloriés ne soient jamais distants d’une unité ? Attention, une seule couleur est utilisée ici et deux points non coloriés peuvent très bien être distants d’une unité.
Pour répondre au problème de Moser, on peut bien sûr centrer un disque ouvert (sans le bord) de rayon 1/2 en tout point de coordonnées paires. La proportion du plan coloriée est alors de π / 16, soit environ 19,63 %.
Utiliser un réseau de points disposés en triangles équilatéraux de côté 2 améliore déjà bien les choses : la proportion du plan coloriée est alors
de soit environ 22,67 %.
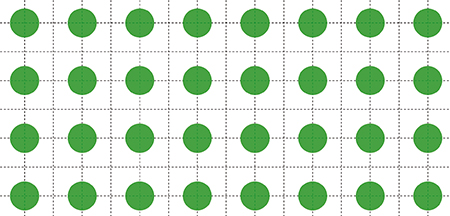
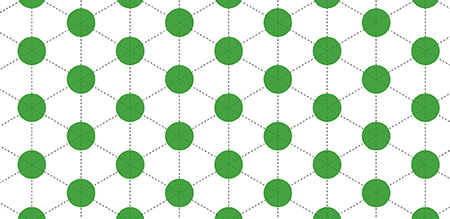
Avec un réseau carré (en haut), le résultat n’est pas optimal :
la surface occupée n’est que d’environ 19,63 %.
Le réseau hexagonal (en bas) donne un résultat d’environ 22,67 %.
Qui dit mieux ? Hallard Croft, en 1967. Le mathématicien de l’université de Cambridge intersecte le disque de rayon 1 / 2 avec un hexagone régulier de hauteur x légèrement inférieure à 1, obtenant ainsi une figure dont la forme évoque pour certains une tortue. Il suffit ensuite de disposer ces tortues sur un réseau hexagonal de côté 1 + x. Le calcul de la proportion est un peu plus délicat : elle est donnée par
Une étude de fonction permet d’établir que le maximum est atteint pour x 0,96553 et cette « tortue de Croft » donne une proportion d’environ 22,94 % ! Jusqu’à ce jour, rien de mieux n’a été proposé.
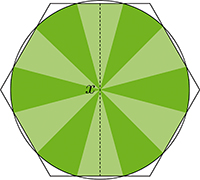
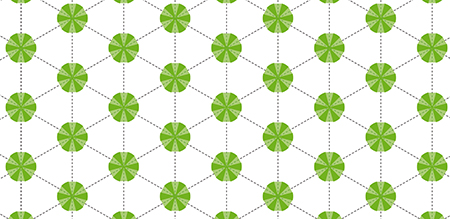
La « tortue de Croft » permet d’atteindre le meilleur résultat connu à ce jour.
5, 6 ou 7 ?
C’est le mathématicien américain Edward Nelson qui aurait le premier proposé à la sagacité de ses homologues la recherche du nombre chromatique du plan en 1950. Onze ans plus tard, le Suisse Hugo Hadwiger a popularisé le problème en publiant une liste de questions ouvertes. Depuis, on parle souvent du problème de Hadwiger‒Nelson.
La majoration du nombre chromatique du plan par 7 a vite été découverte par John Isbell. Pour justifier une telle majoration, exhiber un coloriage valide suffit. C’est le cas ici en considérant un pavage du plan par des hexagones de diamètre légèrement inférieur à 1 et en les coloriant de façon périodique.
Ce n’est qu’en 2018 qu’Aubrey de Grey a découvert un graphe imposant dont toutes les arêtes sont de longueur 1 mais qui nécessite cinq couleurs pour être colorié. Sa première version comptait plus de vingt mille sommets ; il a ensuite réussi à simplifier la situation en ramenant ce nombre à 1 581.
Dans la foulée, la simplification du graphe a fait l’objet d’un projet Polymath. Depuis, la taille du graphe proposé a été réduite à un peu plus de cinq cents sommets, mais la question initiale demeure entière : cinq, six ou sept couleurs pour colorier le plan ?
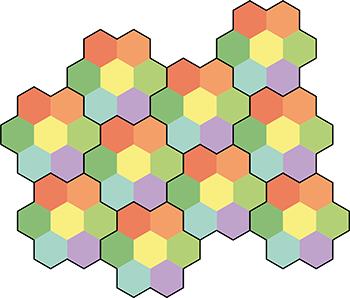
Ce coloriage du plan par des hexagones de diamètre légèrement inférieur à 1
montre que \leqslant 7.)
Prenons le problème par en haut
Faute de trouver un meilleur taux de remplissage en évitant la distance unité, on peut essayer de donner un majorant de cette densité maximale. Appelons A une région coloriée du plan ne contenant aucun couple de points distants d’une unité. Si l’on translate cet ensemble A d’un vecteur unitaire, l’image obtenue ne contient aucun point en commun avec A. On en déduit donc que la proportion du plan occupée par A est inférieure ou égale à 50 %.
Ce premier résultat, presque trivial, peut être amélioré sans trop de peine. Notons et
deux vecteurs unitaires engendrant un triangle équilatéral. L’ensemble A et ses images par les translations de vecteurs
et
sont disjointes, donc A ne peut pas occuper plus du tiers du plan.
Une belle astuce permet d’obtenir des résultats encore plus probants. Pour cela, utilisons un graphe unitaire, c’est-à-dire un graphe dont toutes les arêtes sont de longueur 1. Le fuseau de Moser peut faire l’affaire pour un premier exemple. Notons M1 à M7 ses sommets et regardons les images de l’ensemble A par les sept translations de vecteurs pour j allant de 1 à 7. Aucun point du plan ne peut être recouvert par trois de ces copies de A. Pourquoi cela ? Supposons que ce soit le cas pour un point x. Cela voudrait dire qu’il existe trois points Mi, Mj et Mk du graphe de Moser tels que les points
et
soient dans A. Or, regardez bien, lorsque l’on choisit trois sommets du graphe de Moser, il y en a au moins deux qui sont distants d’une unité. Il y aurait donc au moins deux des trois points xi, xj et xk qui seraient distants d’une unité, ce qui n’est pas possible dans l’ensemble A. Chaque point du plan n’étant recouvert que par au plus deux des sept copies de A, la proportion occupée par l’ensemble A n’excède pas 2 / 7, soit environ 28,57 % du plan. Voilà donc une habile façon de ramener notre problème de coloriage sur le plan (infini) à l’étude de graphes unitaires finis !
Dans les années 1980, le mathématicien hongrois László Székely a envisagé une autre piste de travail. Considérons toujours un ensemble A du plan ne contenant aucun couple de points distants d’une unité. Pour chaque vecteur x du plan, on appelle f (x) la proportion du plan occupée par l’intersection de A et A + x, l’image de A par la translation de vecteur x. Évidemment, f (0) est la proportion du plan occupée par A. Si x est un vecteur unitaire, on a f (x) = 0. L’idée est alors d’étudier cette fonction, dite d’autocorrélation. Il n’est pas trop restrictif de supposer que A est un ensemble périodique (au sens où il existe deux translations de vecteurs non colinéaires qui laissent A invariant). La fonction f devient alors elle-même périodique, ce qui permet de sortir tout l’outillage de l’analyse harmonique ! On peut alors traduire certaines contraintes du problème sous forme de conditions sur les coefficients de Fourier de la fonction f . C’est par ce biais que László Székely a démontré que la proportion du plan occupée par A ne pouvait excéder 12 / 43, soit environ 27,91 %.
Des progrès récents
Au vu de ces premiers résultats, Paul Erdös (1913‒1996), grand émetteur de conjectures s’il en est, a suggéré qu’il n’était sûrement pas possible de dépasser 25 %. Il s’en est suivi une course effrénée vers cette borne, chacun la faisant tendre vers ces satanés 25 % sans jamais y arriver complètement. En 2016, un travail mené via l’analyse harmonique a permis de baisser la borne à environ 25,88 %. Deux ans plus tard, en exploitant les graphes unitaires, la borne est passée à environ 25,65 %. En 2022, l’analyse harmonique a repris le dessus et donné une borne de 25,44 %.
Finalement, les mathématiciens Gergely Ambrus, Adrián Csiszárik, Máté Matolcsi, Dániel Varga et Pál Zsámboki ont combiné toutes les techniques existantes, ramené le problème à une question de programmation linéaire, fait tourner quelques ordinateurs en exploitant des algorithmes d’intelligence artificielle, puis de plus classiques programmes de recherche arborescente, et ont obtenu, dans un article mis en ligne (sur l’archive ouverte arXiv, en juillet 2023), un résultat magistral : la proportion du plan occupée par un ensemble ne contenant aucun couple de points distants d’une unité ne peut pas excéder 24,70 %. La barre des 25 % a été pulvérisée !
Une bien belle réponse vient donc d’être donnée à la conjecture d’Erdös, mais l’aventure ne s’arrête pas là. Il reste encore à rapprocher cette borne et celle de la « tortue de Croft ». Et la question se généralise bien sûr aux dimensions supérieures. Les nouvelles techniques développées ici pourraient même insuffler de nouvelles idées pour la question du nombre chromatique du plan. Avis aux amateurs !
Le nombre d’indépendance d’un graphe
Le raisonnement suivi dans l’article pour établir, grâce au graphe de Moser, que la proportion occupée par une partie du plan ne contenant aucun couple de points distants d’une unité est inférieure ou égale à 2/7 se généralise facilement. Il faut pour cela faire appel à la notion de nombre d’indépendance d’un graphe.
Pour un graphe donné G, on peut considérer un ensemble de sommets qui ne sont pas adjacents. C’est ce qu’on appelle un ensemble indépendant. Parmi tous les ensembles indépendants d’un graphe, on peut en choisir un qui contient un maximum de points. C’est ce nombre que l’on appelle nombre d’indépendance du graphe, et que l’on note souvent α(G). En choisissant un graphe G unitaire (c’est-à-dire dont toutes les arêtes sont de longueur 1) et à n sommets, le même raisonnement que celui suivi pour le fuseau de Moser permet de conclure que la proportion occupée par une partie du plan ne contenant aucun couple de points distants d’une unité est inférieure ou égale à α(G)/n. Hélas, le calcul de α(G) est loin d’être facile et les graphes unitaires qui seraient de « bons » candidats se font rares !
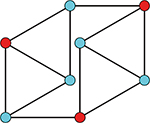
Pour ce graphe, on peut se convaincre rapidement que α(G) = 3.
La majoration obtenue pour notre problème est alors de 3 / 8, soit 37,5 %,
ce qui est une piètre majoration.
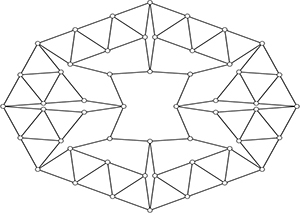
Pour ce graphe (le graphe de Harborth), le calcul est déjà plus délicat.
références
• Les graphes. Bibliothèque Tangente 54, 2015. • The density of planar sets avoiding unit distances. Gergely Ambrus, Adrián Csiszárik, Máté Matolcsi, Dániel Varga et Pál Zsámboki, 2023, disponible en ligne.


