Il n’est pas certain que ce monumental traité que sont les Éléments (fin du IVe siècle avant J.-C.) ait été écrit entièrement par Euclide, personnage mystérieux, dont on ne sait, par ailleurs, quasiment rien. Mais ce qui est sûr, c’est que cet ouvrage, constitué de treize livres, a posé les bases d’une approche axiomatique des mathématiques, influençant considérablement leur développement et, plus généralement, celui de la science. Les quatre premiers livres des Éléments posent les bases de la géométrie plane et étudient des figures comme le triangle et le cercle. Les deux suivants (livres V et VI) étudient les proportions. Ensuite, les livres de VII à X traitent davantage de l’arithmétique et les trois derniers s’intéressent à la géométrie dans l’espace. C’est principalement dans le livre VI que l’on aborde les applications des proportions à la géométrie.
La difficulté des incommensurables
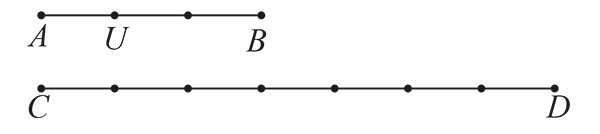
Chez les Grecs, une grandeur en mesure une autre (plus grande) lorsque cette dernière est constituée d’un certain nombre de fois la première. Ainsi, sur la figure ci-après, le segment AU mesure le segment AB, la longueur de ce dernier est triple ; ce même segment AU mesure CD. AB et CD ont une mesure commune, AU, on les dit commensurables.
Sept fois AB égale trois fois CD, on dit aussi que AB mesure CD : la longueur de CD étant égale à 7/3 de celle de AB.
Les nombres entiers rendent compte de la commensurabilité. Or cette conception ne peut pas être universelle. La rencontre par les pythagoriciens avec l’incommensurabilité de la diagonale d’un carré par rapport à son côté marque un échec de cette vision de la proportionnalité. Dès lors, comment comparer ou manipuler des rapports qui, pour eux, ne sont même pas des nombres ?
Quelques siècles plus tard, assimilant les travaux d’Eudoxe de Cnide (IVe siècle avant J.-C.), une théorie des proportions constitue le livre V des Éléments. On y trouve la définition : « Des grandeurs sont dites être en même raison (proportionnelles), la première à la seconde, et la troisième à la quatrième, lorsque des équimultiples quelconques de la première et de la troisième, et d’autres équimultiples quelconques de la seconde et de la quatrième sont tels, que les premiers équimultiples surpassent, chacun à chacun, les seconds équimultiples, ou leur sont égaux à la fois, ou plus petits à la fois. »
Avec les mots d’aujourd’hui, on écrirait : quatre grandeurs a, b, c, d étant dans cet ordre, a est à b comme c est à d (on noterait même ) à condition que, pour tous les entiers n et m (non nuls), on ait
• si na = mb alors nc = md (1)
• si na > mb alors nc > mb
• si na < mb alors nc < mb.
Le seul cas envisageable était celui d’un multiplicateur qui soit un nombre rationnel. La condition (1) ne vaut qu’en cas de commensurabilité. Le génie d’Eudoxe est d’avoir, avec cette définition, d’allure peu naturelle, admis l’incommensurabilité.
Euclide pose un préalable pour les grandeurs envisagées, c’est d’avoir une raison entre elles définissable : a et b étant deux grandeurs, il sera toujours possible de trouver un entier p (non nul) tel que pa > b. Du fait de l’usage par Archimède, on parlera de grandeur archimédienne.
Avec son infinité d’opérations pour valider une proportionnalité, sans recours à l’algèbre, la définition n’est pas aisée à mettre en œuvre. Longuement discutée, plus ou moins bien comprise au fil des siècles, elle reste un joyau théorique avant une définition des nombres réels en fin de XIXe siècle.
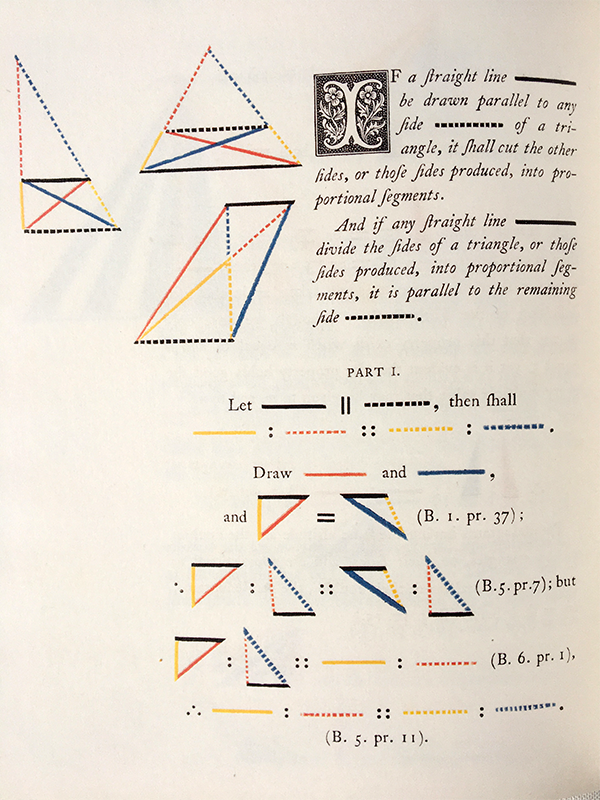
Pour illustrer cette difficulté, considérons la proposition 1 du livre VI où Euclide démontre une propriété qui lui servira par la suite et qui nous paraît facile avec notre conception moderne du nombre : dans le triangle ABD (voir la figure), si C est un point de [BD] alors
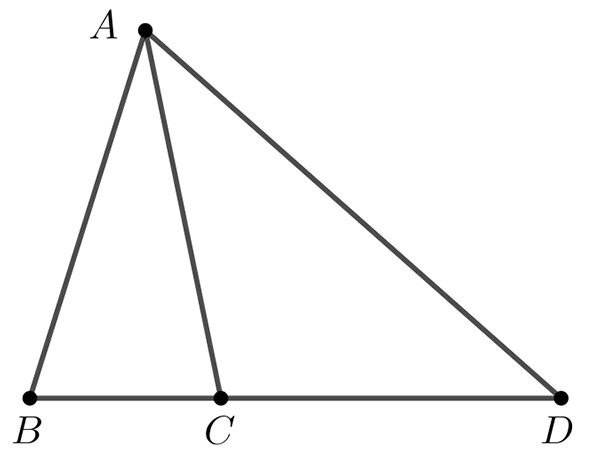
Aujourd’hui, sa démonstration nous semble un trésor de sophistication (voir l’encadré).
Des triangles de même hauteur
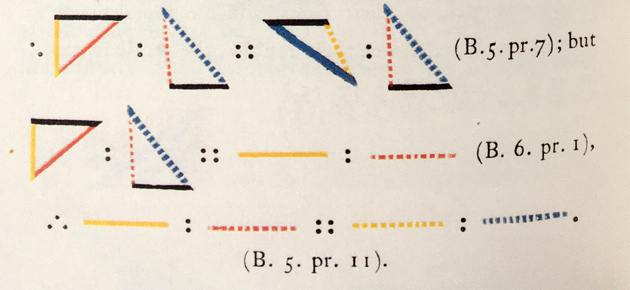
Dans la figure ci-dessous, la hauteur issue de A est la même dans les deux triangles ABC et ACD. Or le livre VI s’ouvre sur une proposition concernant les triangles ayant cette propriété : « Les triangles et les parallélogrammes qui ont la même hauteur sont entre eux comme leurs bases (proposition 1, livre VI) ».
Qu’est-ce à dire ? Que l’aire des triangles est proportionnelle à leur base. Euclide compare des rapports (ou raisons). Avec les triangles ABC et ACD de base BC et CD sur la même droite, il écrit « ABC est à ACD comme BC à CD » (sous-entendant qu’il s’agit d’aires et de longueurs).
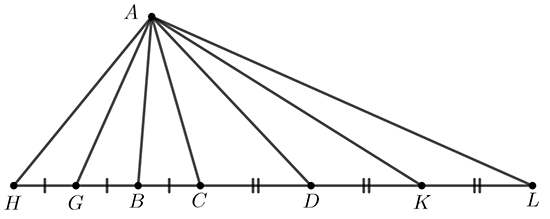
Euclide considère des équimultiples de chacun des triangles (triples sur la figure) ; ainsi des équimultiples de la base BC (une longueur) et du triangle ABC (une aire), avec GB et GH égalant BC. Les triangles ABG, AGH et ABC, ayant des bases de même longueur, ont même aire. Avec cette terminologie, le triangle ACH est triple de ABC. De même, ACL est triple de ACD.
Euclide constate alors que :
• si la base HC est égale à la base CL, le triangle AHC sera égal au triangle ALC ;
• si la base HC surpasse la base CL, le triangle AHC surpassera le triangle ALC ;
• si la base HC est plus petite que la base CL, le triangle AHC sera plus petit que le triangle ALC.
D’où la proportion, le triangle ABC est au triangle ACD comme la base BC est à la base CD.
On notera le recours à l’emploi d’un « cas générique » : Euclide n’évoque que des triples et non des équimultiples quelconques, comme si cela valait généralité.
Pour un théorème célèbre
De cette proposition 1 découle une belle démonstration d’un autre théorème célèbre : « Si l’on conduit une droite qui soit parallèle à un des côtés d’un triangle, cette droite coupera proportionnellement les côtés de ce triangle ; et si deux côtés d’un triangle sont coupés proportionnellement, la droite qui joindra les sections sera parallèle au côté restant du triangle (proposition 2, livre VI). » On reconnaît notre théorème de Thalès.

Pour le triangle ABC et la droite (DE ) parallèle à (BC ), les triangles BDE et CDE ont même aire car ils ont même base DE et même hauteur (distance des deux droites (BC ) et (DE )). D’après la proposition 1, en aires et longueurs,
et
L’égalité des aires BDE et CED implique
La droite coupe les côtés proportionnellement.
La réciproque – la proportion implique le parallélisme – sera démontrée de même par Euclide avec, implicitement, le fait que D est entre A et B, et E entre A et C.
Chez Euclide, la proportionnalité apparaît également à travers l’étude des figures semblables qu’il définit de la manière suivante : « Les figures rectilignes semblables sont celles dont les angles sont égaux chacun à chacun et dont les côtés placés autour des angles égaux sont proportionnels (première définition du livre VI). »
Qu’en est-il des aires ? « Les triangles semblables sont entre eux en raison doublée des côtés homologues » (proposition 19). Il s’agit du lien entre les aires, « raison doublée » voulant dire « élévation au carré ». Pas si simple de lire Euclide dans le texte !