Proportionnalité et géométrie
Dès l’origine, la proportionnalité, que l’on trouve en algèbre avec la règle de trois, est devenue incontournable en géométrie. On la rencontre pour démontrer l’incommensurabilité de certaines longueurs ou évaluer des aires et des volumes. Chez Euclide, elle est un outil indispensable pour de nombreuses démonstrations. Très liée aux configurations de parallélisme, via le fameux théorème de Thalès, elle donnera lieu à de célèbres résultats, comme les théorèmes de Ceva ou de Ménélaüs. Moins connus, l’antiparallélisme et les rapports associés ont ouvert la voie à de nouvelles approches. On leur doit la puissance d’un point par rapport à un cercle ou la transformation d’inversion.

LES ARTICLES
Redécouvrir la proportionnalité
M. Brilleaud et A. Houlou-Garcia
Quand on pense proportionnalité, on pense souvent règle de trois, c’est-à-dire à une technique de calcul. Pourtant, cette notion est d’abord apparue en géométrie, avec l’étude des figures semblables à la base de nombreux théorèmes, et où elle a fait émerger l’idée de grandeurs incommensurables.
Chez Euclide
Jean Aymès
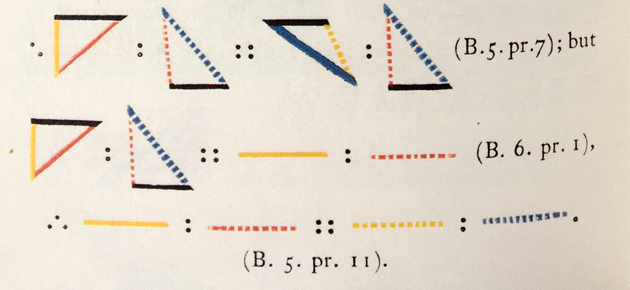
Pour les géomètres de l'Antiquité, l'impossibilité de concevoir des nombres non rationnels a posé des problèmes pour la manipulation de rapports entre des longueurs ou des aires qui ne sont pas obligatoirement commensurables. La définition que l'on trouve dans les Éléments d'Euclide est restée en vigueur jusqu'au XIXe siècle.
Les enfants de Thalès
Élisabeth Busser
En géométrie élémentaire, de nombreuses démonstrations font appel à la proportionnalité. Presque tous les théorèmes mythiques de la discipline sont concernés : Thalès, Ptolémée, Ménélaüs, Ceva, Pappus… Petit tour de ces grands problèmes.
Les curiosités de l’antiparallélisme
Anne Boyé
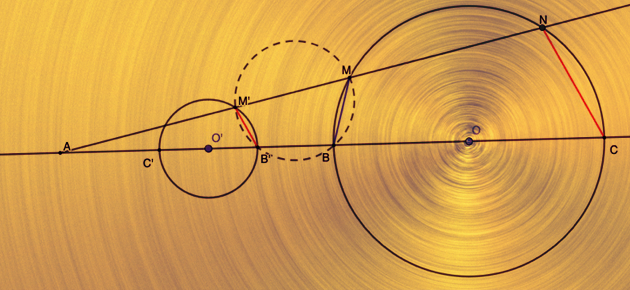
En géométrie élémentaire, la notion de proportionnalité fait souvent intervenir des droites parallèles, en référence au théorème de Thalès. Il existe aussi des droites antiparallèles. Y aurait-il alors une « antiproportionnalité » ?