Étudier
Pour un mathématicien, comprendre les surfaces, c'est en général faire de la géométrie différentielle ou du calcul intégral. Que de progrès réalisés depuis les anciens Grecs, qui devaient recourir à de redoutables astuces adaptées à chaque cas rencontré !
Pour le praticien aux prises avec un cas déterminé, par exemple l'étude de la surface terrestre, la question se pose plutôt de trouver des outils spécifiques à la surface particulière à étudier. De la virologie aux bulles de savon, les cas concrets ne manquent pas. Des questions variées se posent, dont les impacts sont souvent insoupçonnés, débouchant parfois sur des applications considérables.
Pour le praticien aux prises avec un cas déterminé, par exemple l'étude de la surface terrestre, la question se pose plutôt de trouver des outils spécifiques à la surface particulière à étudier. De la virologie aux bulles de savon, les cas concrets ne manquent pas. Des questions variées se posent, dont les impacts sont souvent insoupçonnés, débouchant parfois sur des applications considérables.

LES ARTICLES
Dès que l'on quitte le domaine des figures élémentaires, le calcul d'aire se heurte à la notion d'infini. Après Archimède et son utilisation habile de l'infini potentiel, il fallut attendre la Renaissance pour que le verrou cède pour de bon.
« Le géoïde, une surface unique »
Interview de Xavier Campi
Benoît Rittaud
La surface qui nous est la plus familière, celle que nous arpentons quotidiennement, pose son lot de questions : quelle est précisément la forme de la Terre ? Ce n'est pas exactement une sphère, ni un ellipsoïde. Cet objet irrégulier, le géoïde, possède des propriétés parfois subtiles. Interview d'un spécialiste de la question.
Exquises surfaces minimales
Hervé Lehning
Une surface est minimale lorsque, son bord étant fixé, son aire est la plus petite possible. Une réalisation physique des surfaces minimales est offerte par les bulles de savon.
Le virus conquérant
Jacques Bair
L'étude de l'action des virus passe également par… la géométrie. En particulier, déterminer la surface conquise par un virus permet d'évaluer sa dangerosité. Alors munissons-nous d'un microscope ! Direction le laboratoire pour quelques travaux pratiques…
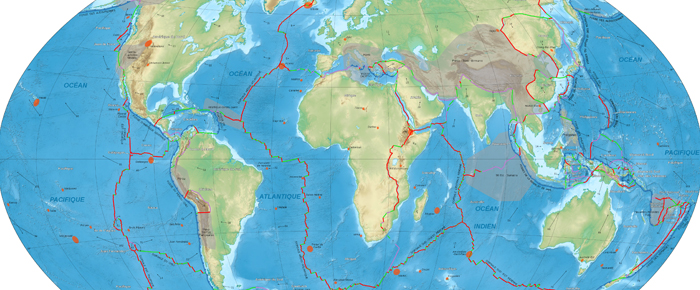
De la tectonique des plaques à l'habillage de la sphère
Daniel Justens
La surface de notre planète semble constituée d'une croûte dure. Mais comment se représenter ce recouvrement d'une sphère ? La tectonique des plaques montre que la surface terrestre se compose de plaques dures en mouvement, se frottant les unes aux autres.