Une référence très ancienne, dans un traité sur la poésie sanskrite du mathématicien indien Pingala, datant de 450 avant notre ère, décrit le fameux trilatère comme « l'escalier du Mont Meru ». En Italie, c'est le triangle de Tartaglia ; au Moyen Orient, on parle du triangle de Khayyám ; en Chine, on s'émerveille devant le triangle de Yanghui.

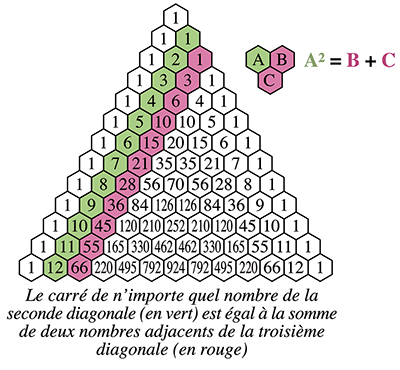
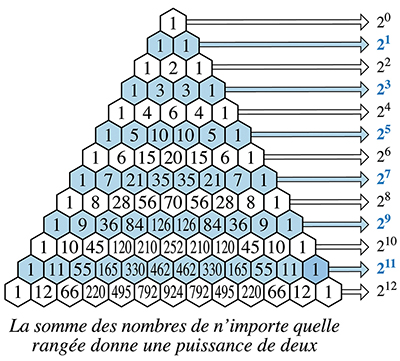
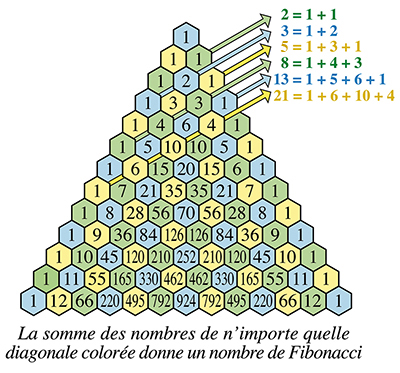
Qu'importe ! Dans le « triangle de Pascal », le chiffre 1 apparaît une infinité de fois. Tous les autres nombres apparaissent un nombre fini de fois. Ceux qui se rencontrent plus de quatre fois sont très rares. Par exemple, le plus petit nombre qui apparaît six fois est 120, tandis que 3 003 est le plus petit nombre apparaissant huit fois. Mais d'autres curiosités sont moins connues…

Enfin, en noircissant les cases où apparaît un entier impair, on obtient une image analogue au triangle de Sierpi?ski. Un motif fractal similaire apparaît en noircissant toutes les cases non congrues à 0 modulo un nombre premier p.

Un poster affichant ces triangles est disponible en ligne.