Des pyramides de nombres premiers

Construisons des pyramides ! Non pas celles d’Égypte, qui ont nécessité une main-d’œuvre gigantesque et malléable, mais des pyramides de nombres… Alors des entiers, oui, mais pas n’importe lesquels ! Nous allons bâtir avec des nombres premiers qui, en plus, devront être palindromes en base 10, c’est-à-dire que leur écriture décimale doit pouvoir se lire de la même manière de gauche à droite et de droite à gauche. C’est le cas de 2, 3, 5, 7, évidemment, puisqu’ils ne possèdent qu’un seule chiffre, mais également de 11 ou de 151 par exemple. On ignore s’il existe une infinité de nombres premiers palindromes (on conjecture que c’est bien le cas).

Partons depuis l’élément le plus modeste, un simple chiffre, qui représentera le sommet de la pyramide. Ajoutons ensuite en escalier des nombres premiers successifs. La règle sera que chaque nombre d’un étage reprendra le nombre de l’étage immédiatement au-dessus, en y ajoutant une « marche », soit un chiffre nouveau des deux côtés, de façon symétrique.

Mettons-nous en jambes avec une première petite pyramide :

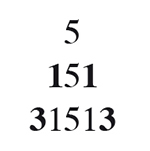
À chaque étape, il faudra évidemment tester la primalité du nombre écrit !

Vingt-trois siècles vous contemplent…

Pour un début de pyramide donné, il peut exister plusieurs façons de poursuivre la construction. Ainsi, les deux architectures suivantes conviennent :

À un moment donné, il arrivera que la pyramide s’arrête par manque de nombre premier palindrome. Le but du jeu consistant à construire la pyramide la plus haute, il sera alors permis d’ajouter plus qu’un chiffre à chaque extrémité de l’escalier, comme illustré sur l’exemple suivant.

Une des plus hautes pyramides numériques trouvées à ce jour est la suivante :

Saurez-vous faire mieux ?