S’orienter dans un labyrinthe n’est jamais simple. Il y a plusieurs techniques pour en sortir : celle de « la main droite », celle de l’algorithme de Pledge, celle de l’algorithme de Trémeaux… Les nombres aussi jouent parfois à faire de tortueux dédales pour nos méninges, dont il est bien difficile de s’échapper !
Quand les suites s’en mêlent
La suite mathématique L ci-dessous, proposée par Lars Blomberg, fut difficile à produire. C’est une sorte de labyrinthe à une seule dimension. Parcourir ce labyrinthe est enfantin… mais son issue est à l’infini.
L = 1, 3, 0, 5, 7, 9, 2, 20, 13, 15, 4, 18, 31, 38, 33, 35, 21, 8, 34, 37, 23, 17, 19, 6, 11, 78, 28, 50, 51, 25, 61, 39, 29, 81, 10, 16, 53, 27, 80, 14, 55, 57, 22, 59, 83, 30, 58, 85, 65, 12, 43, 70, 40, 71, 32, 52, 41, 73, 45, 47, 72, 42, 75, 49, 24, 54, 77…
En voici le mode d’emploi :
Entrez par la gauche et placez-vous sur le chiffre 1 ; ce 1 est impair, vous devez donc sauter vers la droite par-dessus un chiffre ; vous atterrissez sur 0 ; ce zéro est pair, vous devez donc sauter vers la gauche par-dessus zéro chiffre ; vous atterrissez sur 3 (le voisin de gauche du zéro) ; ce 3 est impair, vous devez donc sauter vers la droite par-dessus trois chiffres ; vous atterrissez sur 9 ; ce 9 est impair, vous devez donc continuer vers la droite, franchir neuf chiffres et atterrir sur le 8 de 18 (ce ne sont pas des nombres qu’il faut enjamber, mais des chiffres) ; ce 8 est pair, vous sautez donc vers la gauche par-dessus huit chiffres et atterrissez sur 2 ; lequel vous envoie sur 5, etc.
À la fin de l’exercice vous aurez parcouru toute la suite.
Trois règles ont présidé à la construction de L : (1) tous les termes de L sont positifs et distincts ; (2) L est la lexicographiquement première de toutes les suites de ce type possibles ; (3) les « îlots » sont interdits. Qu’est-ce qu’un îlot ? Quelque chose comme [1, 0, 3, x, y, z, 4] où l’on voit qu’entrer par 1 vous mène à 3, puis 4, puis 0 puis 1 à nouveau : on tourne en rond ! Comme dans certains labyrinthes physiques conçus pour tromper la technique de « la main droite ». Cette suite porte le numéro A285471 dans l’OEIS, l’encyclopédie en ligne des suites d’entiers de Neil Sloane et Simon Plouffe.
Restons dans les labyrinthes. Une autre suite mathématique récente de l’OEIS (A328931, due à David Lawrence et Andrew Howroyd) compte tous les parcours possibles dans des labyrinthes carrés aux cellules carrées. Si les labyrinthes 1 × 1 et 2 × 2 sont triviaux, on sent un frémissement avec le 3 × 3 où quatre parcours différents sont possibles (aux symétries et rotations près) :
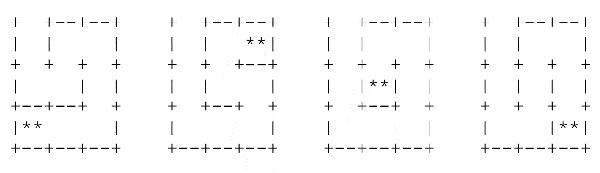
Ensuite c’est l’explosion combinatoire : il y a 441 809 773 825 445 785 471 324 877 668 710 façons de parcourir le « bête » labyrinthe 15 × 15 (soit le plateau d’un jeu de Scrabble traditionnel). On ignore le nombre de parcours distincts pour n > 15 : avis aux amateurs !
Un cavalier qui surgit…
Voici un dernier labyrinthe qui n’est pas sans évoquer les membres de l’Ouvroir de littérature potentielle, lesquels se définissent souvent comme « rats qui construisent eux-mêmes le labyrinthe dont ils se proposent de sortir ». Il s’agit du parcours d’un cavalier d’échecs sur un échiquier infini dont les cases sont numérotées, dans l’ordre, selon une spirale carrée. Le cavalier commence au centre de l’échiquier, sur la case 1, et saute (comme aux échecs) sur la case à sa portée qui affiche le nombre le plus petit. La surprise vient du fait que le cavalier s’auto-emprisonne ! Après deux mille seize sauts, il n’a plus aucune case où sauter, elles sont toutes occupées.
À l’entrée A316328 de l’OEIS, des variantes permettent à ce cavalier de s’ébattre à l’infini. Elles sont dues à Maximilian Hasler, sur une idée originale de Neil Sloane en personne (la vidéo « The Trapped Knight » de la chaîne Numberphile, disponible sur Youtube, illustre ces propriétés).

