Des performances moyennes en hausse


Michel Criton


Lorsqu’on déplace un élément d’un ensemble vers un autre, les valeurs moyennes des deux ensembles sont généralement modifiées. Si l’une augmente, l’autre doit-elle automatiquement diminuer ? Paradoxalement, ce n’est pas toujours le cas.

Les clubs sportifs des villes de Nordcité et de Sudaigne ont chacun une section « marathon » comprenant quatre coureurs ou coureuses. Le tableau ci-dessous donne les performances des athlètes exprimées en minutes. On supposera que ces performances sont régulières et stables dans le temps.

 

 

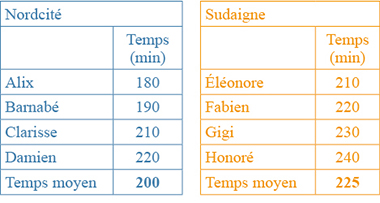
Mais Damien déménage, quitte Nordcité, s’installe à Sudaigne et s’inscrit, naturellement, au club sportif de cette ville. Les performances des deux équipes sont désormais les suivantes.

 

 

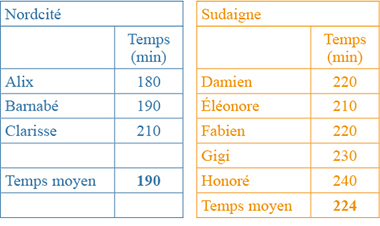
Suite à ce changement de club de Damien, on constate que les temps moyens des deux clubs se sont améliorés puisqu’ils ont tous deux diminué !

 

Ce paradoxe est connu sous le nom de phénomène de Rogers, du nom de l’acteur et scénariste américain William Penn Adair Rogers (1879‒1935). Dans une boutade célèbre, il déclara que si le moins intelligent des habitants de l’Oklahoma (où il est né) déménageait pour s’installer en Californie, les quotients intellectuels moyens des habitants des deux États augmenteraient !

 

 

Le phénomène de Rogers

 

Après une migration d’une personne du club sportif X vers Y, les performances moyennes des deux clubs ont toutes les deux augmenté. Est-il alors possible qu’une autre migration de Y vers X fasse à nouveau augmenter les performances moyennes x et y des deux clubs ? Voyons pourquoi ce n’est pas possible. Soit m la performance du sportif migrant de X vers Y. On doit nécessairement avoir x < m < y. Soient x’ et y’ les nouvelles performances moyennes des deux clubs (avec x’ < y’) et m’ la performance d’une personne migrant de Y vers X. On devrait avoir m’ > y’ et m’ < x’, ce qui est contradictoire.

 

Dans la bourgade de Centreville, il existe trois clubs sportifs. Dans chacun, les adhérents sont classés en cinq niveaux : 0 (grands débutants), 1, 2, 3, 4 et 5 (champions). Le tableau suivant résume les nombres d’adhérents de chaque niveau et le niveau moyen pour chacun de ces trois clubs.

 

 

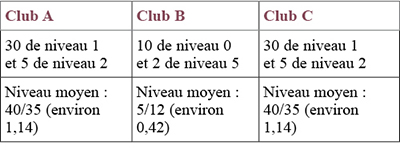
Suite à des assemblées générales orageuses, les trente adhérents de niveau 1 du club A claquent la porte et s’inscrivent au club B, et un adhérent de niveau 5 du club B quitte le navire et décide d’aller cotiser au club C. La nouvelle composition des associations est la suivante.

 

 

 

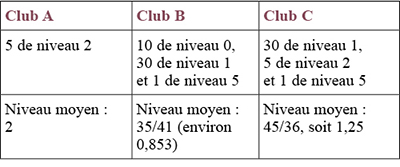
2. Est-il possible que de nouvelles migrations de C vers B et de B vers A aient pour résultat une nouvelle amélioration du niveau moyen des trois clubs ?