Dans une note de la seconde édition des Problèmes plaisants et délectables qui se font par les nombres, Claude-Gaspard (parfois orthographié Claude-Gaspar) Bachet de Méziriac expose une méthode de résolution de l'équation indéterminée du premier degré à deux inconnues.

Cet exposé laisse clairement apparaître que l'auteur connaissait le théorème dit de Bezout. Voici la méthode de Bachet appliquée sur un exemple, telle qu'il la présente.
Trouver le premier multiple de 211 qui surpasse de 10 un multiple de 1 007.
Il s'agit, en termes modernes, de trouver la plus petite solution en nombres entiers de l'équation indéterminée 211x = 1 007y + 10.
Bachet utilise un algorithme que l'on reconnaîtra, puisqu'il s'agit de l'algorithme d'Euclide (que l'on arrête dès que le nombre cherché est obtenu). Il procède de la façon suivante :
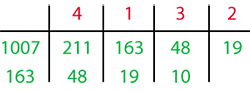
• il divise 1 007 par 211 ; le quotient est 4 et le reste 163 ;
• il divise 211 par 163 ; le quotient est 1 et le reste 48 ;
• il divise 163 par 48 ; le quotient est 3 et le reste 19 ;
• il divise 48 par 19 ; le quotient est 2 et le reste 10 (nombre que l'on voulait atteindre).
Une mécanique bien huilée
Bachet recopie ensuite les quotients dans l'ordre sur une ligne (en rouge).

Sur une deuxième ligne, à droite du dernier quotient (égal à 2), on écrit le nombre 1, et 0 à droite du 1. Puis on calcule :
1 × 2 + 0 = 2. On écrit 2 à gauche du 1.
2 × 3 + 1 = 7. On écrit 7 à gauche du 2.
7 × 1 + 2 = 9. On écrit 9 à gauche du 7.
9 × 4 + 7 = 43. On écrit 43 à gauche du 9.
La solution du problème est 43 × 211 = 9 × 1 007 + 10.
Si l'on veut trouver d'autres solutions de l'équation 211x = 1 007y + 10, il suffit de considérer l'ensemble des couples (x, y) = (43 + 1 007k, 9 + 211k) où k est un nombre entier relatif quelconque. On obtient ainsi une infinité de solutions.
À vous de jouer : appliquez la méthode de Bachet aux équations suivantes :
a) 14x = 9y + 1.
b) 18x = 93y + 1.
Pourquoi dans le cas de cette équation la méthode de Bachet n'aboutit-elle pas ?
c) 18x = 93y + 15.
La méthode de Bachet ne permettra pas d'aboutir à 15, mais elle permet d'obtenir un diviseur d de 15. On obtient ainsi un couple solution de l'équation 18x = 93y + d. Il suffira ensuite de multiplier les valeurs obtenues par 15 / d pour obtenir le couple solution cherché.

