La jeune Epsilon se demande encore ce qui l’a conduite à accepter de retrouver son ami Bêta dans un local à vélo poussiéreux de l’Institut intergalactique, à deux heures du matin, pour l’assister… dans l’improbable accomplissement d’un rituel de magie noire. Le garçon doit réussir une session de rattrapage avec le professeur Phi le lendemain et a jugé que son salut passait par des pratiques moins conventionnelles que la révision assidue de ses cours. Epsilon ne croit pas en la magie, mais elle sait aussi que le problème principal de Bêta vient de son manque de confiance en lui. Peut-être qu’un rituel, même s’il n’a rien de magique, pourrait l’aider sur cet aspect ? La détresse profonde dans le regard de Bêta : voilà, au fond, ce qui l’a poussée à dire oui.
Rites et arithmétique
Un livre à l’épaisse couverture en cuir noir est ouvert sur le sol. Un pentagramme s’étale sur une page, accompagné d’instructions. Une craie, une pile de bougies et une boîte d’allumettes sont posées à côté.
« Il faut que l’on dessine un pentagramme parfait, explique Bêta, histoire de mettre toutes les chances de mon côté. Mais je n’ai rien prévu pour tracer ne serait-ce qu’un trait bien droit… »
Epsilon avise une planche de bois aux bords réguliers et une tige en métal, sans doute un rayon de roue cassé. Elle décroche la courroie flexible de son sac et l’attache à une extrémité de la tige avant de prendre la craie des mains de Bêta et de la coincer dans le mousqueton à l’autre bout de la corde improvisée.
« Voilà, annonce-t-elle, nous avons à présent une règle et un compas. Je vais tenir la tige et tu vas pouvoir tracer un cercle bien rond sur le sol. »
Bêta s’exécute tandis qu’Epsilon poursuit ses explications : « Si nous arrivons à tracer un pentagone régulier inscrit dans ce cercle, nous aurons gagné la partie : il suffira d’en relier les différents sommets pour obtenir notre pentagramme. Pour placer cinq points régulièrement espacés sur un cercle, nous devons le découper en cinq secteurs angulaires égaux. Le tour complet valant 2π radians, nous avons besoin de construire des angles de 2π / 5 radian. »
Elle s’empare alors d’un morceau de craie et esquisse un schéma approximatif au sol.
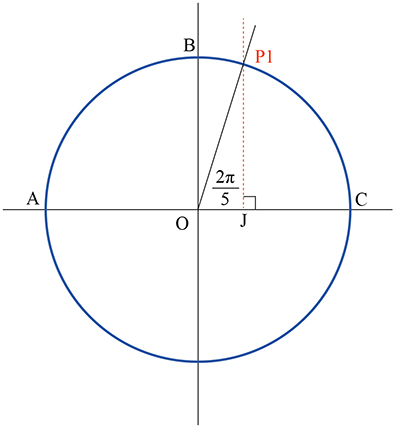
« Si l’on considère que notre cercle est un cercle de rayon 1, nous devons trouver ce point J tel que OJ = cos (2π / 5).
– À quoi cela nous avance-t-il ? dit Bêta en se grattant la tête. Ta règle ne sert qu’à tracer des droites et sans doute des angles droits, mais je n’ai rien pour mesurer…
– Attends, ça va devenir joli ! On a précisément vu pendant le cours sur les nombres complexes d’hier que cos (2π / 5) = Re(z), où z = exp (2iπ / 5) = cos (2π / 5) + i sin (2π / 5),
Re(z) désignant sa partie réelle. Comme z5 = 1, on sait que z est une racine du polynôme X5 – 1, qui se factorise en (X—1)(X4 + X3 + X2 + X + 1). Et puisque z est différent de 1, z vérifie aussi z4 + z3 + z2 + z + 1 = 0. On a également z différent de 0 donc on peut diviser l’égalité précédente par z². Avec un petit jeu d’écriture, on se ramène à :
(z + 1 / z)2 + (z + 1 / z) – 1 = 0.
– Mais… pourquoi tout ça ? balbutie Bêta, passablement effaré.
– Eh bien, parce que tu vérifieras que cos(2π/5) = (z + 1/z)/2, et que l’on sait donc, grâce à cette relation, que 4 cos2(2π/5) + 2 cos(2π/5) – 1 = 0. »
Pouvez-vous, cher lecteur, en déduire une expression numérique de cos(2π/5) ? Et, à partir de là, trouver un point J qui convienne en utilisant uniquement les instruments d’Epsilon et une pincée de Pythagore ? Tracer un pentagramme ne devrait ensuite plus rien avoir de diabolique…
Un sabbat mathématique
Une fois la figure achevée, c’est au tour d’Epsilon d’observer avec incrédulité la danse frénétique de Bêta au milieu des bougies disposées aux sommets du pentagramme parfait. À un moment, elle sent même un courant d’air envelopper ses épaules, et en tournant la tête, elle jurerait avoir vu une ombre se glisser le long de la porte.
Le lendemain, quand elle demande à Bêta comment s’est passé son examen avec le professeur Phi, son camarade lui répond : « Notre rituel a marché comme sur des roulettes ! Tu sais en quoi consistait l’énoncé de l’exercice ? Il s’agissait de construire une étoile à cinq branches régulière à la règle et au compas… »

