La structure hexagonale (en nid d’abeilles) a la particularité de présenter des alignements de cases dans trois directions. À partir d’un hexagone unique, on peut entourer cet hexagone d’une ou plusieurs couches d’hexagones identiques. On obtient ainsi des configurations d’ordre 2, 3, 4, etc., l’ordre étant le nombre d’hexagones sur un côté de la structure.
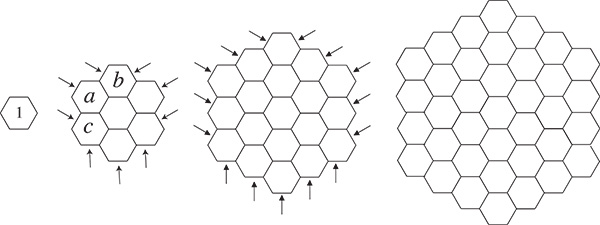
Ces configurations permettent-elles de construire des figures magiques, en écrivant dans caque case un nombre entier, de telle sorte que la somme des nombres écrits dans les cases de n’importe quelle rangée soit toujours la même ? Si, de plus, les entiers utilisés sont les entiers consécutifs à partir de 1, on aura alors affaire à une figure magique dite normale.
L’hexagone d’ordre 1 est un cas trivial.
Existe-t-il un hexagone magique normal d’ordre 2 ? La réponse est négative. En effet, on ne peut avoir a + b = a + c (voir la figure) que si b = c. L’hexagone ne peut alors être normal, toutes les cases du pourtour ne pouvant prendre que deux valeurs et la case centrale ne pouvant contenir que le nombre 0 pour que les sommes de trois nombres soient égales aux sommes de deux nombres.
1. Un hexagone d’ordre n comprend 2n – 1 rangées dans chacune des trois directions. Montrez qu’il contient 3n × (n – 1) + 1 cases. Quelles sont les valeurs de n pour lesquelles un hexagone magique normal est théoriquement possible ?
Un hexagone normal d’ordre n contient les entiers de 1 à 3n × (n – 1) + 1.
La somme S de ces entiers est égale à [3n(n – 1) + 1] × [3n(n – 1) + 2]/2.
En développant, on obtient S = (9n4 – 18n3 + 18n2 – 9n +2)/2.
Cette somme doit être divisible par 2n – 1, le nombre de rangées dans chacune des trois directions.
La somme S peut aussi s’écrire (2n – 1) × (9n3/2 – 27n2/4 + 45n/8 – 27/16) + 5/16.
La constante magique M est égale à
S/(2n – 1) = (9n3/2 – 27n2/4 + 45n/8 – 27/16) + 5/[16(2n – 1)].
On a alors 16M = (72n3 – 108n2 + 90n – 27) + 5/(2n – 1).
Le premier terme est un entier et le second n’est entier que si n = 1 ou 3, ce qui établit qu’aucun hexagone magique normal ne peut exister hors de ces valeurs.
Une solution pour n = 3 ?
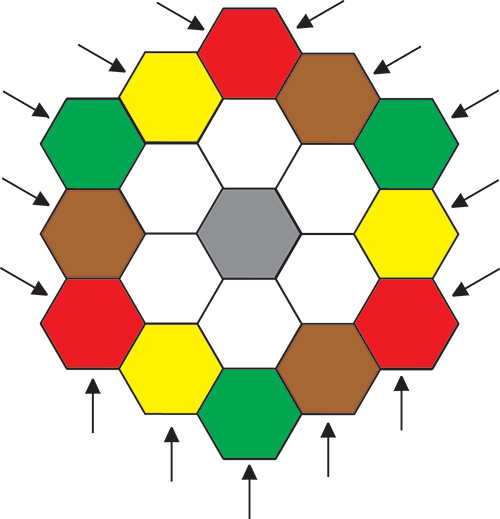
Cet hexagone compte 19 cases dans lesquelles on doit essayer de placer les nombres entiers de 1 à 19, dont la somme est égale à 190. La somme magique M est ici égale à 190/5, soit 38.
Appelons g l’entier occupant la case grise, R la somme des entiers situés dans les cases rouges, V celle des entiers dans les cases vertes, J celle des entiers dans les cases jaunes, N celle des entiers dans les cases noisette et B celle des entiers dans les cases blanches. Nous avons V + J + R = 3M = 114. On en déduit que N + B + g = 190 – 114 = 76.
Si on additionne les sommes de trois rangées de 4 cases formant un triangle, on compte deux fois les nombres des cases jaunes ou deux fois ceux des cases noisette :
3 × 38 = 2N + B, d’où N = 38 + g.
On montre de façon similaire que J = 38 + g.
En remplaçant N par 38 + g dans l’égalité N + B + g = 76, on obtient B = 38 – 2g.
Le système obtenu est indéterminé, mais en comparant N, somme de trois nombres, égal à 38 + g, et B, somme de six nombres, égal à 38 – 2g, on observe que la moyenne des nombres des cases noisette est supérieure ou égale à 13, tandis que celle des nombres des cases blanches est inférieure ou égale à 6. On en déduit également que g est au plus égal à 8.
Il a été démontré qu’il existe un seul hexagone magique normal d’ordre 3, à rotation et symétrie près.
2. Complétez l’hexagone.
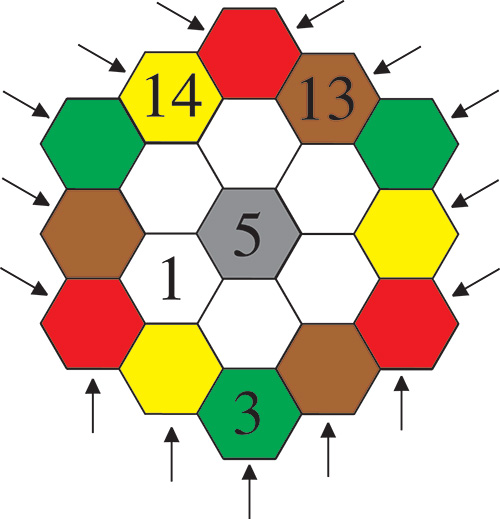
Des hexagones magiques non normaux pour n ≥ 4 ?
Il faut noter que si l’hexagone magique normal d’ordre 3 est unique, à rotation et symétrie près, il en existe de non normaux où les entiers utilisés sont tous différents, mais ne sont pas les entiers de 1 à 19. Pour n ≥ 4, on sait qu’il n’en existe pas de normaux, mais peut-il en exister avec des entiers consécutifs ne commençant pas par 1 ?
La réponse à cette question est positive. Prenons l’exemple d’un hexagone d’ordre n = 4, qui comprend 37 cases et 7 rangées de cases dans chaque direction.
Si le plus petit entier est k, la somme de 37 entiers consécutifs commençant pas k est égale à (36 + k)(37 + k)/2 – k(k – 1)/2, soit 666 + 37k.
Cette somme doit être divisible par 7, donc (666 + 37k)/7 doit être un entier ;
(666 + 37k)/7 = 95 + 5k + (2k + 1)/7.
Ce n’est le cas que lorsque k est congru à 3 modulo 7. Il faut bien sûr vérifier que de tels hexagones magiques existent, ce qui est le cas, l’exemple suivant correspondant à k = 3.
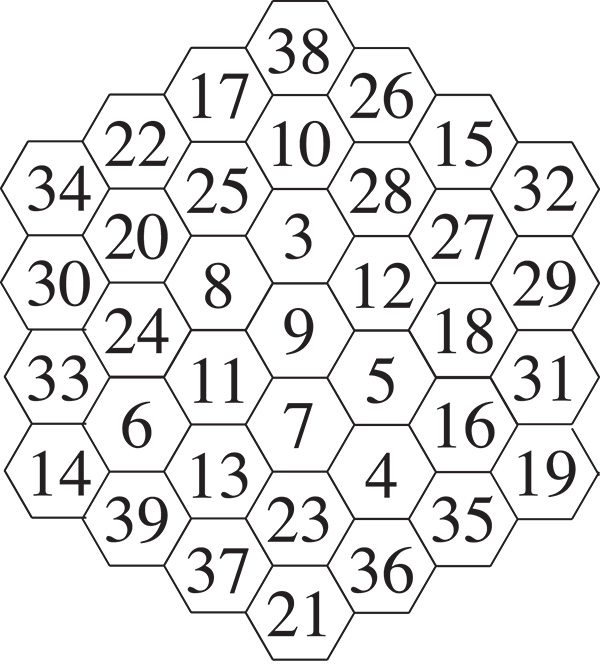
SOURCES
- A Unique Magic Hexagon. Charles W. Trigg, Recreational Mathematics Magazine, 1964.

