SOLUTION
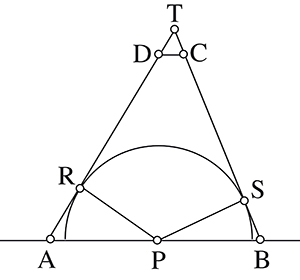
Soient R le point de contact entre le cercle et [AD], S le point de contact entre le cercle et [BC], et T l’intersection des droites (AD) et (BC). On sait que les angles et
sont des angles droits.
On a PR = PA × sin = PS = PB × sin
, d’où PB / PA = sin
/ sin
.
Par ailleurs, sin / sin
= BT / AT = BC/AD.
On en déduit : (AB – PA) / PA = BC/AD, soit 92 / PA – 1 = 5 / 7, d’où l’on tire PA = 161 / 3. On a donc m + n = 164.

