Les nombres sont à la base des mathématiques. Les entiers naturels ont été introduits pour résoudre des problèmes de dénombrement, puis d'autres nombres ont été étudiés pour résoudre des problèmes de plus en plus variés et profonds. Or, le concept apparemment combinatoire, arithmétique de nombre admet une interprétation géométrique intéressante grâce à la droite numérique.
Des extensions des nombres naturels
Les nombres entiers naturels (1, 2, 3…) permettent de compter des objets en faisant abstraction des propriétés particulières de ceux-ci. Selon une citation du mathématicien Leopold Kronecker (1823-1891), « Dieu a créé les entiers, les hommes ont fait le reste ». Si l'on ajoute ou multiplie entre eux deux entiers naturels, le résultat fournit encore un naturel. Mais les deux opérations fondamentales d'addition et de multiplication ne peuvent être inversées qu'au prix de sévères restrictions ; par exemple, la soustraction 1 – 2 ou la division sans reste n'ont pas de sens lorsque l'on se limite aux naturels. En créant d'une part le zéro et les entiers négatifs, et d'autre part les nombres fractionnaires, on a libéré la soustraction et la division de leurs entraves, avec la réserve que la division par 0 reste dénuée de signification. Les nombres rationnels sont ainsi les nombres entiers ou fractionnaires, positifs, nuls ou négatifs. Chacun d'entre eux peut s'écrire sous la forme a0,a1a2a3… , où a0 désigne un entier relatif (muni d'un signe) tandis que a1, a2, a3… sont des chiffres décimaux, la virgule séparant donc la partie entière de la décimale. La représentation décimale de tout rationnel est soit limitée (en ce sens qu'elle comprend un nombre fini de chiffres décimaux), soit illimitée mais périodique. Les nombres rationnels sont soumis aux règles familières de l'algèbre (ils forment un corps commutatif totalement ordonné).
Malheureusement, il n'existe pas assez de rationnels pour répondre à tous les besoins des mathématiciens. C'est pourquoi on a introduit les nombres irrationnels, qui admettent une représentation décimale illimitée et non périodique. Les nombres réels sont constitués de tous les nombres rationnels ou irrationnels. Chacun d'entre eux admet donc une représentation décimale, limitée ou illimitée (périodique ou non). Très utilisés en analyse classique, ils sont aussi nombreux que les points d'une droite et se manipulent algébriquement comme les rationnels (ils forment eux aussi un corps totalement ordonné, incluant d'ailleurs celui des rationnels, mais qui est cette fois complet en un sens bien précis).
Hyperréels et autres non standards
Il n'existe aucun réel strictement positif inférieur à tous les autres réels strictement positif (si un tel réel a existait, on aurait l'absurdité a < a / 2). Pour combler une telle lacune pourtant utile pour résoudre des problèmes rencontrés en analyse, Gottfried Wilhelm Leibniz (1646-1716) et ses successeurs vont exploiter des nombres non réels qualifiés d'infiniment petits positifs : ceux-ci sont effectivement strictement positifs, mais plus petits que tout réel strictement positif ; on peut en prendre l'opposé, ce qui donne des infiniment petits négatifs, ou l'inverse, ce qui fournit des nombres infiniment grands (c'est-à-dire supérieurs à n'importe quel réel). On peut encore les ajouter à un réel x quelconque, de manière à former des nombres infiniment proches de x. L'existence de tous ces nouveaux nombres a été justifiée par le mathématicien canadien Abraham Robinson au XXe siècle (voir Tangente 149) ; en effet, dans les années 1960, ce dernier les a construits effectivement en faisant appel à un raisonnement rigoureux mais assez sophistiqué (en utilisant le concept mathématique d'ultrafiltre).
Ces nombres infiniment petits (positifs ou négatifs), infiniment grands (positifs ou négatifs) et infiniment proches d'un réel forment, avec tous les réels, l'ensemble des nombres hyperréels. Ceux-ci se manipulent algébriquement avec les mêmes règles de calcul que les réels (ils forment également un corps commutatif totalement ordonné, englobant celui des réels) et sont à la base de l'analyse dite non standard. Un élève de Robinson, Albert Harold Lightstone (1926–1976), a établi que le nombre 0,999…, possédant une partie entière nulle et s'écrivant avec un nombre infiniment grand de chiffres décimaux tous égaux à 9, est tel que la différence 1 – 0,999… est un infiniment petit positif ; ce résultat confirme la croyance intuitive, rencontrée chez de nombreux débutants en analyse, selon laquelle 0,999… est « un petit peu plus petit » que 1.
Dites-le avec des droites
Considérons maintenant une droite déterminée par deux de ses points X et X'. Elle peut être parcourue dans deux sens opposés. On convient d'en choisir un, de X' vers X, qui est appelé le sens positif, l'autre étant évidemment qualifié de négatif. Le sens positif est matérialisé par une flèche placée sur la droite même, qui prend alors le nom d'axe orienté. On se donne ensuite une unité de longueur u pour la mesure des segments portés par l'axe. La mesure de tout segment [AB] est toutefois affectée du signe + ou – suivant que [AB] est parcouru de A vers B dans le sens positif ou négatif de l'axe ; on attribue de la sorte au segment une mesure algébrique, .
Dans cet exemple, et
On choisit arbitrairement un point O sur la droite (X'X) ; ce sera l'origine de l'axe. La mesure 0 lui est associée. On adjoint le nombre 1 au point situé à l'extrémité du segment issu de l'origine et de mesure algébrique égale à 1, et le nombre – 1 à son symétrique par rapport à O. Puis on attribue le nombre 2 à l'extrémité du segment partant de O et de mesure algébrique 2, et, bien entendu, – 2 à son symétrique par rapport à O. En continuant de la sorte, les entiers positifs et négatifs sont tous représentés par des points équidistants sur l'axe orienté, les positifs d'un côté de l'origine et les négatifs de l'autre côté. Ces points peuvent être qualifiés d'entiers et être identifiés aux nombres entiers relatifs (munis d'un signe).
Semblablement, on peut donner une interprétation géométrique aux nombres fractionnaires de dénominateur égal à l'entier naturel n. Il suffit en effet de diviser en n parties égales chaque segment de longueur unitaire situé entre deux entiers successifs : les points de subdivision forment, avec les points entiers, des points qui peuvent être appelés points rationnels. Chacun d'eux est dès lors caractérisé, de façon univoque, par un nombre rationnel.
Un nombre rationnel a est alors inférieur à un autre rationnel b si, et seulement si, le point représentatif de a est situé « à gauche » du point associé à b. L'ordre naturel des nombres coïncide donc parfaitement avec celui des points correspondants sur l'axe orienté ! Par ailleurs, les points rationnels sont denses sur la droite (X'X), ce qui revient à dire que tout segment de l'axe non réduit à un point, de longueur aussi petite fût-il, contient des points rationnels.
Des trous partout
S'il est vrai qu'à tout nombre rationnel correspond un et un seul point rationnel de l'axe, la réciproque n'est pas vraie ! En d'autres termes, les points rationnels ne « remplissent » pas la droite en question. En effet, les géomètres grecs de l'Antiquité ont montré qu'il existe des points P de l'axe pour lesquels la longueur du segment [OP] est incommensurable avec l'unité de longueur u, en ce sens que ces deux grandeurs n'ont pas de « commune mesure ». Ceci se traduit numériquement par le fait que la mesure algébrique n'est pas un nombre rationnel. C'est le cas, par exemple, pour le point P extrémité de la diagonale [OP] d'un carré de côté égal à l'unité u et disposé comme sur la figure.
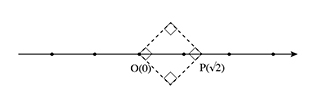
D'après le théorème de Pythagore, OP2 = 2. On peut dès lors adjoindre au point P le nombre √2, solution positive de l'équation x2 = 2. Ce nombre n'est pas rationnel.
Plus généralement, en associant à tout point non rationnel de la droite (X'X) un (unique) nombre, qualifié d'irrationnel, tout point de l'axe est caractérisé par un et un seul nombre rationnel ou irrationnel. Ce nombre sera appelé l'abscisse du point en question. Ainsi, tout point de l'axe est caractérisé par une (unique) abscisse réelle, c'est-à-dire rationnelle ou irrationnelle. Au total, il y aura précisément autant de nombres réels que de points sur la droite. En outre, les nombres et les points peuvent être, en quelque sorte, « identifiés ». L'axe (X'X) est naturellement appelé droite numérique réelle.
Mais l'ensemble des nombres réels est inclus dans celui des nombres hyperréels. Il est dès lors assez normal d'essayer de représenter géométriquement ces derniers à partir de la droite numérique réelle !
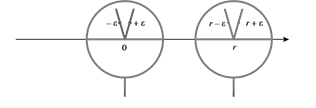
Déjà, les hyperréels non réels ne sont pas directement repérables sur l'axe (X'X), puisque les points de cette droite correspondent exactement aux réels. Toutefois, certains hyperréels peuvent être imaginés virtuellement en utilisant une « loupe infiniment puissante » pointée sur l'origine de la droite classique. On découvre ainsi, par cette expérience de pensée, des nombres invisibles à l'œil nu (et donc non réels), mais infiniment petits puisque infiniment proches de 0. Ils forment le halo de 0. Sur la figure suivante, le halo de 0 est matérialisé symboliquement par deux sortes d'antennes situées au-dessus de l'origine O de la droite réelle et contenant les nombres infiniment petits inférieurs ou supérieurs à 0. On observe aussi, sur cette même figure, ce que l'on obtient en déplaçant la loupe pour la centrer sur un nombre réel r quelconque : apparaissent alors des nombres non réels qui sont infiniment proches de r, tels que les nombres r + et r –
, et qui forment le halo de r.
Par ailleurs, il existe des hyperréels infiniment grands, positifs ou négatifs. Ils ne peuvent pas être observés à l'œil nu sur la droite numérique réelle, mais on peut les imaginer au moyen d'une « jumelle infiniment puissante dirigée le plus loin possible » vers la droite ou vers la gauche. En procédant de la sorte, on peut se représenter par la pensée des nombres respectivement infiniment grands positifs ou infiniment grands négatifs, comme par exemple les nombres 1 / et – 1 /
, où
est un infiniment petit.
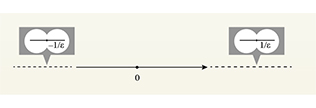
Au total, l'utilisation de loupes ou des jumelles infiniment puissantes permet de se représenter virtuellement les nombres hyperréels associés aux points de ce que l'on pourrait appeler une droite numérique hyperréelle. Celle-ci est composée des points de la droite numérique réelle, chacun de ceux-ci étant accompagné de tout un halo de points infiniment proches, ainsi que des points « infiniment éloignés » situés vers la droite ou vers la gauche.