
Prenez un segment. Jusque-là, rien de passionnant. Coupez-le en trois et supprimez la partie centrale pour construire un triangle équilatéral, comme sur la figure ci-dessous.
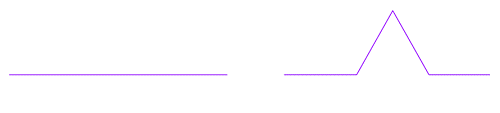
C’est déjà un peu plus joli. Et si on répétait le processus sur chacun des segments obtenus ?

La figure produite en répétant cette simple transformation indéfiniment est peut-être l’exemple le plus connu d’image fractale ; chaque partie est identique au tout. En partant d’un triangle équilatéral, on obtient le flocon de von Koch.

Le Suédois Niels Fabian Helge von Koch (1870–1924), qui s’est beaucoup intéressé à la théorie des nombres, a proposé cet objet comme exemple de courbe continue sans tangente. La longueur de la courbe étant multipliée par 4/3 à chaque étape, celle-ci diverge vers + alors que l’aire délimitée par le flocon, dont la valeur exacte s’obtient par sommation des termes d’une suite géométrique, est finie !
Ce phénomène n’est pas déconnecté de toute réalité. Les parois de l’intestin ou des alvéoles pulmonaires permettent ainsi de maximiser les échanges avec l’extérieur en offrant une très grande surface de contact dans un volume restreint.
Des tapis, des éponges…
On peut obtenir bien d’autres figures en choisissant une autre transformation à ... Lire la suite
