
On sait déjà écrire 2021 à la manière de Takeshi Kitano, avec neuf chiffres (2021 = - 1 + 2 × 3 + 4 × 567 × 8/9), ou seulement cinq, comme le suggère Alain Zalmanski (2021 = (1 + 2)!! + (3!)4 + 5).
On sait aussi, contrairement à ce qu’imaginait Leonhard Euler en 1772, que, s’écrivant x² + x + 41 (avec x = 44), comme l’a fait remarquer Fabien Aoustin, il aurait pu être premier… mais non, puisque 2021 = 43 × 47. C’est donc une différence de deux carrés (452 – 22), des nombres chers à Pierre de Fermat.
On sait encore, comme le dit Gaël Octavia, que 2021 est la somme de quarante-sept (tiens, tiens…) nombres consécutifs : 2021 = 20 + 21 + … + 65 + 66. Il peut aussi, en cherchant bien, comme le signale François Lavallou, être palindrome, puisqu’en base 46, 2021 s’écrit XX avec X = 43.
Mais 2021 a bien d’autres tours dans son sac ! Voulez-vous l’écrire de manière non triviale en base 10 avec un seul chiffre ? Voilà :
et ça marche avec tous les chiffres de a = 1 à a = 9.
Préférez-vous avec un seul exposant ? On a 2021 = 122 + 162 + 422 = 22 + 212 + 262 + 302, ou 2021 = 13 + 13 + 13 + 13 + 73 + 73 + 113, ou encore 2021 = 14 + 14 + 14 + 24 + 34 + 54 + 64.
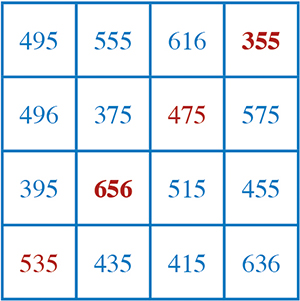
Trouverez-vous vingt-cinq caractéristiques et propriétés de ce carré magique proposé par Alain Zalmanski ?
Envisagez-vous des formes plus sophistiquées, par exemple avec des nombres triangulaires, de la forme ? Parmi les résultats, on retiendra 2021 = T (1) + T (19) + T (60).
Préférez-vous les nombres de la suite de Fibonacci, définis par
F (0) = F (1) = 1, F (n) = F (n – 1) + F (n – 2) pour n ≥ 2 ? Là encore, de nombreuses possibilités vous sont offertes, dont 2021 = F (7) + F (9) + F (14) + F (17).
On doit nombre de ces vues arithmétiques non conventionnelles du millésime de cette année à Inder Jeet Taneja, ancien professeur des universités de Santa Catarina (Brésil) et de New Dehli (Inde), spécialiste de récréations numériques. Il a compilé et mis en ligne un document de plus de soixante-dix pages qui occupera longtemps les amateurs de 2021.
