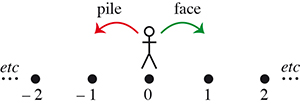
Imaginons un petit jeu, anodin en apparence : plaçons un quidam au milieu du salon, à égale distance des murs situés à sa gauche et à sa droite. Jouons à pile ou face. À chaque résultat face, demandons au quidam de faire un pas vers la gauche, à chaque résultat pile, vers la droite. Après avoir joué dix fois, quelle sera la position du docile promeneur ? Après combien de lancers celui-ci touchera-t-il l’un des deux murs ? Et quel sera ce mur ? Le mur de gauche ? Celui de droite ? Ce jeu peut sembler absurde, les questions qu’il induit sans intérêt. Il est pourtant à la base de l’une des avancées les plus spectaculaires dans l’histoire des mathématiques : l’émergence des processus stochastiques.
Stochastique ou aléatoire ?
L’usage du terme « stochastique » est récent. Jusqu’au milieu du XXe siècle, on parlait plus volontiers de processus aléatoires. Ce changement sémantique traduit un changement drastique de paradigme. L’étymologie l’explique fort bien. Le terme « aléatoire » dérive directement du latin aleatorius, signifiant « relatif au jeu de hasard » ; on y retrouve la racine aleum (le hasard, et par extension le dé, le jeu de dés). Le terme « stochastique » dérive du grec ancien stochastikos, signifiant « conjectural ». On y découvre le substantif stochos, ... Lire la suite
