
Le théorème d’équidécomposabilité
Le mathématicien écossais William Wallace (1768–1843) fut le premier à démontrer cette propriété en 1807. Le Prussien Paul Gerwien, ignorant le résultat de Wallace, le redémontra en 1833 et Farkas Bolyai fit de même en 1835 (voir Découpages et Pavages, Bibliothèque Tangente 64, 2018). La démonstration de ce théorème d’équidécomposabilité repose sur deux propriétés : tout polygone peut être triangulé (divisé en un nombre fini de triangles), et tout triangle peut, après découpage, être réassemblé pour former un rectangle de base donnée.
La construction du puzzle
Dans la littérature, on trouve parfois la construction suivante.
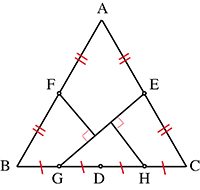
Les points E et F sont les milieux respectifs des côtés [AC] et [AB] et le côté [BC] est partagé en quatre longueurs égales BG, GD, DH et HC. En prenant comme unité la longueur du côté du triangle équilatéral, son aire est égale à , dont la racine carrée est égale à environ 0,658. En calculant la longueur EG, on obtient
, soit environ 0,661. La construction est donc seulement approchée : on obtient non pas un carré, mais un rectangle de côtés
et
, qui diffèrent de moins ... Lire la suite gratuitement
