
L’écriture d'une fraction, comme 31/12, ne permet pas toujours de s’en représenter clairement la valeur. Pour ce faire, on peut avoir recours à son développement décimal, en effectuant la division du numérateur par le dénominateur.
Dans notre exemple, cela donne ceci :
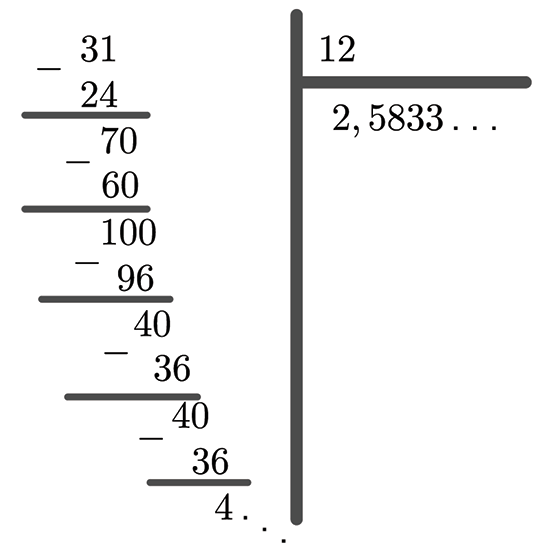
Puisque, à partir d’un certain moment, le reste est toujours égal à 4, le chiffre 3 va s’imposer dans chaque nouvelle décimale du quotient. C’est ainsi que la fraction 31/12 admet un développement décimal illimité, 2,5833333…, qui voit la répétition sans fin du chiffre 3. Plus rigoureusement, on note ce développement, pour indiquer la répétition périodique du chiffre 3. Autrement dit, on a l’égalité
Essayons à présent avec une autre fraction, 75/34. Le début de la division de 75 par 34 donne le quotient
2,2058823529411764705882352941176470588235294117647…
C'est plus compliqué que dans le cas de 31/12, mais on voit tout de même qu’après les deux premiers chiffres (les deux premiers 2), n’apparaît plus que la séquence 0588235294117647, qui se répète encore et encore dans le développement. Pour 75/34 aussi, il y a donc une période. On peut alors écrire
Toujours pareil
En réalité, dans la division d’un entier par un autre, ... Lire la suite
