
Les nombres qui peuvent s’écrire comme le quotient de deux entiers sont qualifiés de rationnels. Même les jeunes enfants comprennent très bien ce que représentent les fractions 1/2, 1/3 ou 3/4 lorsqu’il s’agit de couper un gâteau. L’une des plus fameuses surprises que réserve la géométrie est que la longueur de la diagonale d’un carré de côté 1, égale à n’est pas un nombre rationnel. On le sait depuis l’Antiquité, et on raconte souvent que la démonstration de ce résultat serait due à Hippase de Métaponte, qui aurait ainsi provoqué une crise des fondements chez les pythagoriciens et lui aurait valu d’être noyé !
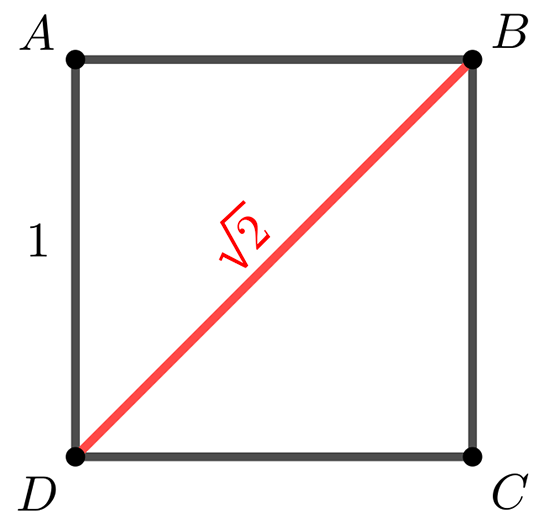
Si ABCD est un carré de côté 1, alors la diagonale [BD] mesure √ 2.
Une chose est sûre : les savants de l’Antiquité grecque se sont intéressés à des questions de cet ordre, et plus exactement au fait que deux longueurs peuvent être incommensurables, c’est-à-dire dans un rapport qui n’est pas rationnel.
Une longue acceptation
Le fait que certaines longueurs ne soient pas exprimables comme quotient de nombres entiers a souvent été vu comme une forme d’échec. Accepter que certains nombres ne soient pas rationnels n’est pas si facile. D’ailleurs, les ... Lire la suite
