
Année du chat noir, 2026 vous réserve trois vendredis 13 : un en février, un en mars puis un en novembre. Pour certains ce sera peut-être l’occasion de tenter sa chance au loto. Dans tous les cas, que les superstitieux de tout poil en profitent car il ne peut pas y avoir plus de vendredi 13 en une seule année.

Peut-être gardez-vous un souvenir prégnant du millésime 2025 qui, en tant que carré d’un nombre triangulaire, recelait de nombreuses propriétés particulièrement élégantes et a même été l’objet de quantités de vidéos ou animations diverses sur les réseaux sociaux. L’année 2026 pourrait sembler plus fade au premier abord, mais détrompez-vous, il y a de quoi s’amuser aussi cette année !
Un petit truc en plus
Contrairement à l’an dernier, 2026 n’est pas un carré. Par contre, 20263 – 20262 en est un (celui de 91 170), ce qui se généralise à tout successeur d’un carré. D’ailleurs 2026 est naturellement la somme de deux carrés (2026 = 2025 + 1) mais c’est surtout la seule façon de le décomposer ainsi comme somme de deux carrés non nuls. Ce n’est pas le cas de tous les entiers de la forme n2 + 1.
Par exemple, 65 = 82 + 1 = 72 + 42 et 2117 = 462 + 1 = 342 + 312. Pierre de Fermat (vers 1605-1665) s’était intéressé de près aux décompositions des entiers en somme de deux carrés, en particulier dans un long courrier daté de Noël 1640 et adressé à « mon révérend Père » Marin Mersenne (1588-1648). Il faudra cependant attendre les travaux de Carl Gustav Jacobi (1804-1851) au XIXe siècle pour être en mesure d’établir une formule donnant le nombre de décompositions en somme de deux carrés d’un entier donné.
Revenons à 2026 et au fait qu’il s’écrive sous la forme n2 + 1, et en particulier que l’entier n en question, à savoir 45, soit impair. En écrivant les entiers sous forme de spirale, les successeurs des carrés impairs apparaissent tous dans le coin inférieur droit.
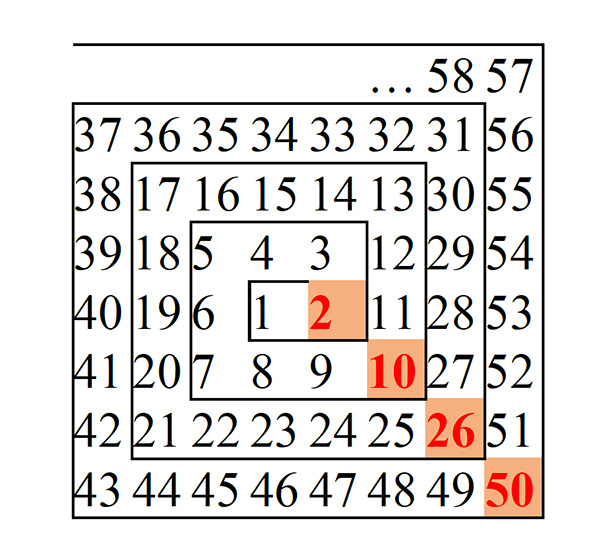
C’est en assistant à une conférence, paraît-il particulièrement ennuyeuse, que Stanislaw Ulam (1909-1984) gribouilla cette spirale en 1963. Il y coloria les nombres premiers et vit ainsi apparaître des motifs assez réguliers qui gardent encore en partie tout leur mystère aujourd’hui.
Un autre lien existe entre 2026 et les nombres de la forme n2 + 1. Si vous partez de 0 et que vous appliquez plusieurs fois la fonction définie par f (n) = n2 + 1, vous finirez par tomber sur un nouveau nombre qui se termine par 0. Cela arrive au bout de six étapes et le résultat est d’ailleurs 458 330. Cela fonctionne aussi en partant de 1 ou 2 mais pas de 3. Pour vous en convaincre, il suffit de faire les calculs : on aboutit dans le cycle (0, 1, 2, 5, 6, 7) qui se répètera indéfiniment sans jamais revenir à 3. Avec 2026 aussi vous finirez par tomber sur un nombre qui se termine par 2026, et cela en six étapes également. Le nombre en question est :
42162622043820589475763301393483294985588850597501496703159869505429422415
40544793505642652181734936693228117322802764824276355718732857750650374248
6145502193136631059483236263981479149047893828475561779562152026. Ouf !
De plus, en itérant la fonction f sur un nombre possédant 4 chiffres ou plus, on aboutit toujours sur un nombre dont les 4 derniers chiffres appartiennent au cycle (4330, 8901, 7802, 1205, 2026, 4677).
Des petits carrés sans lever le crayon
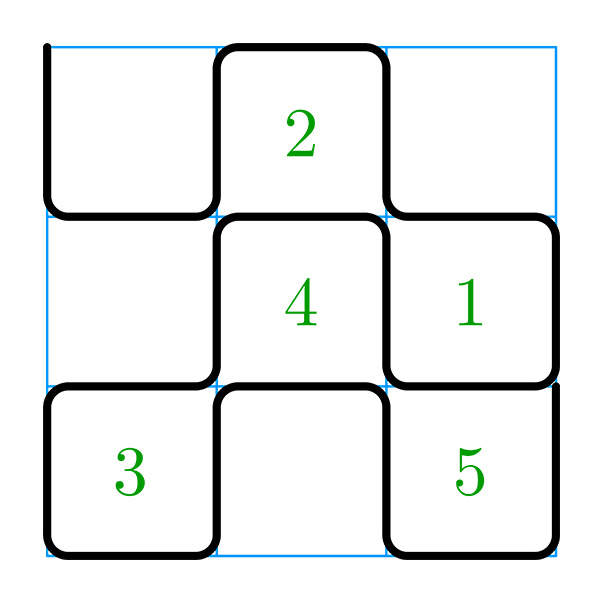
Partez d’un coin d’une grille carrée de côté 3 puis parcourez les segments unité sans lever le crayon et sans jamais repasser par le même segment. Vous devriez réussir à dessiner ainsi 5 carrés de côté 1 mais jamais un de plus. Si vous partez d’une grille de côté 46, vous pourrez atteindre au maximum 2026 petits carrés !
Pléthore de propriétés arithmétiques !
En plus d’être le successeur d’un carré, 2026 est aussi le prédécesseur d’un nombre premier. La prochaine fois que cela arrivera, ce sera en 3250. Notez cependant que 2208 est aussi encadré par un premier et un carré, mais pas dans le même ordre.
Nous avons vu que 2026 s’exprimait d’une seule façon comme somme de deux carrés mais on peut aussi l’obtenir comme somme de sept cubes. Il y a alors neuf solutions possibles : les trouverez-vous toutes ?
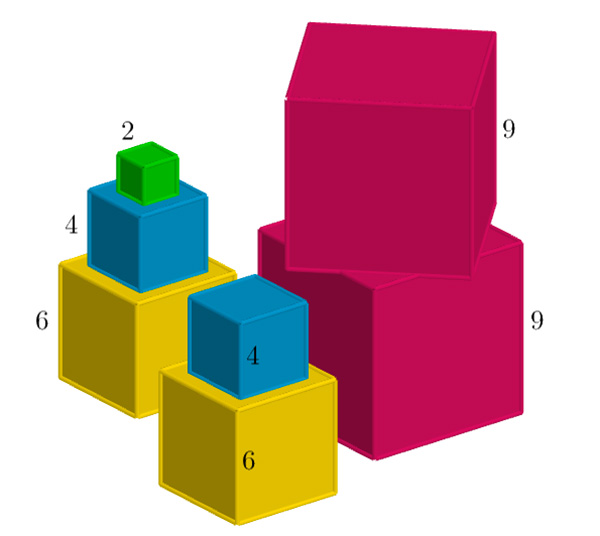
2026 est la somme de 7 cubes.
Si vous tenez à additionner des carrés, il suffit de les choisir judicieusement parmi les 21 premiers :
1² + 2² + 3² + 5² + 6² + 7² + 10² + 11² + 13² + 14² + 15² + 17² + 19² + 21² = 2026.
Chose amusante, ceux qui ont été enlevés ne sont pas n’importe lesquels : ce sont les carrés de 4, 8, 9, 12, 16, 18 et 20. Tous ces entiers sont eux-mêmes divisibles par des carrés. En fait nous n’avons gardé que les 14 premiers entiers sans facteurs carrés, c’est-à-dire les entiers qui ne sont pas divisibles par un carré parfait (autre que 1 bien sûr). Fermat avait d’ailleurs recours à ces entiers sans facteurs carrés pour traiter le fameux problème du théorème de Noël !
Puisque nous évoquons la divisibilité, restons dans le domaine de l’arithmétique où la somme s(n) des diviseurs stricts d’un entier n offre un véritable terrain de jeu pour tout amateur ou amatrice de récréations mathématiques.
On a par exemple s(2366) = 2026 car les diviseurs de 2366 sont 1, 2, 7, 13, 14, 26, 91, 169, 182, 338 et 1183. Les calculs sont un peu plus longs à la main mais on peut aussi vérifier que s(s(4402)) = 2026. En revanche, si vous cherchez un entier n tel que s(s(s(n))) = 2026, vous risquez d’être déçu car il n’en existe pas !
Dans un autre registre, signalons également, que 2026 = 211 – 2 × 11. Cette notation à l’esthétique plaisante peut s’interpréter concrètement. Imaginez que vous vouliez former un groupe de 11 personnes parlant soit chinois, soit français (mais pas les deux) mais sans qu’une personne ne se retrouve seule à parler sa langue. Il y a alors 2026 façons de procéder car pour chaque personne vous avez deux choix de langue (chinois ou français) ce qui donne 211 possibilités auxquelles on va retirer les 11 situations où une seule personne parle français et les 11 situations où une seule parle chinois.
Des dispositions géométriques élégantes
Disposer des points pour former des figures particulières est une activité qui était prisée du temps des pythagoriciens et qui a suscité de l’intérêt bien longtemps. On peut par exemple dessiner des « diamants » en disposant des points sous forme de losange. Voici par exemple les diamants de côté 2, 3 et 4 :
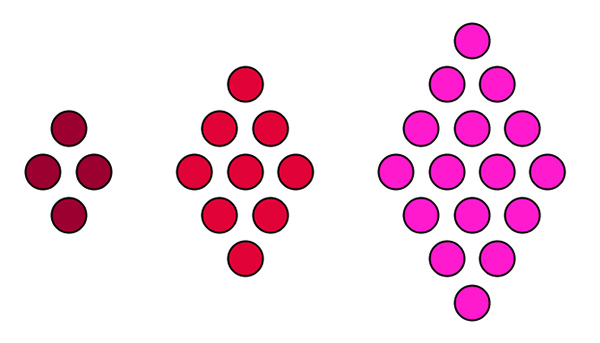
Puisque nous sommes en 2026, assemblons trois diamants de côté 26 par un sommet commun pour donner une forme de triangle équilatéral, ce qui nécessite… 2026 points !

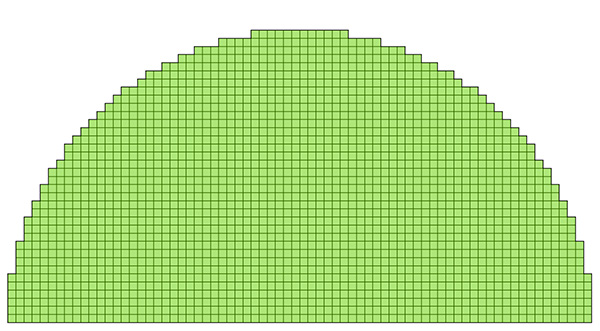
Les images pixelisées sont constituées de petits carrés qu’on peut aussi s’évertuer à dénombrer. Dans le demi-disque ci-dessous, il y en a exactement 2026 !
Les graphes fournissent eux aussi des questions de dénombrement particulièrement relevées. Considérons par exemple tous les graphes quartiques, c’est-à-dire ceux où il existe exactement quatre arêtes en chaque sommet, et parmi ceux-là ne retenons que ceux qui possédent 17 sommets. Il y en a de très jolis et il en existe en tout 86 223 660. C’est énorme mais si on retire tous ceux qui sont connexes, c’est-à-dire constitués d’un seul morceau, alors il n’y en a plus que 2026 !
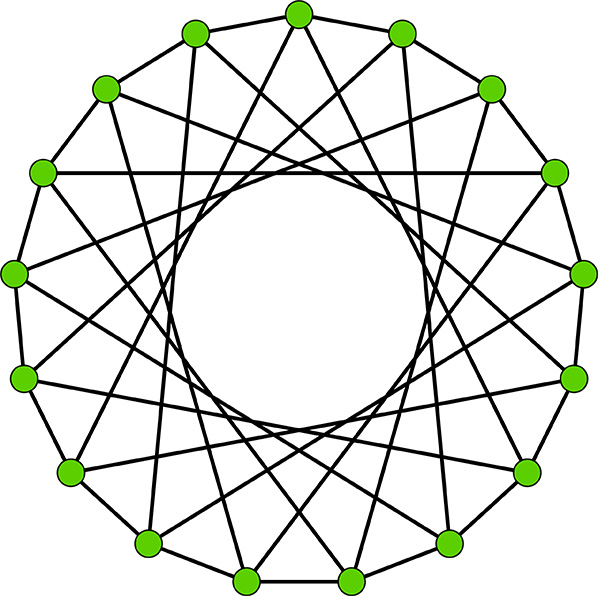
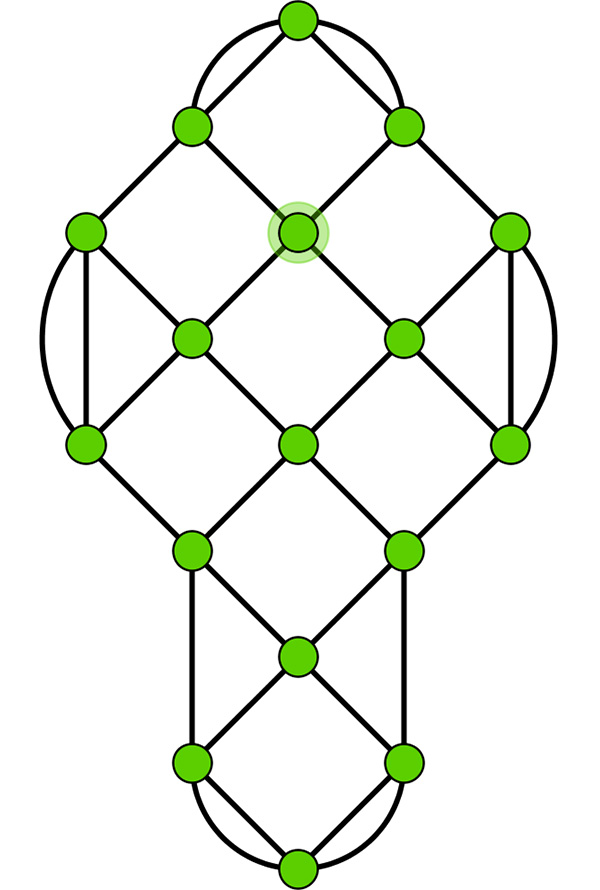
Deux graphes quartiques connexes d’ordre 17.
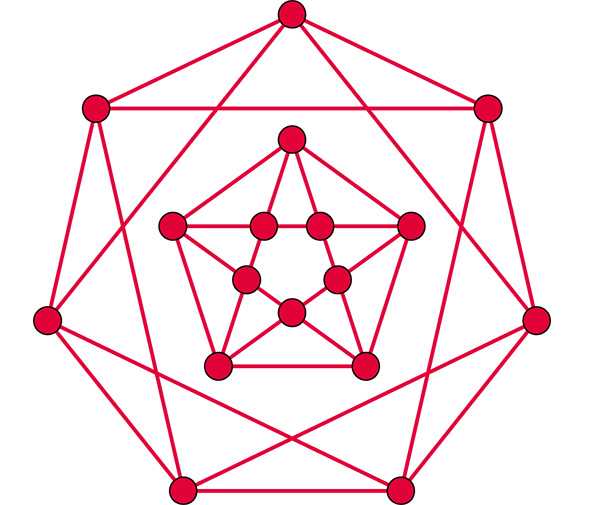
Un graphe quartique non connexe d’ordre 17. Il en existe 2026.
Les formes géométriques essaiment dans tous les champs des mathématiques. Le triangle de Pascal est bien connu mais ses variantes un peu moins. Il suffit pourtant de changer les 1 sur les côtés du triangle de Pascal par d’autres suites de nombres pour obtenir un nouveau territoire à explorer. Voici par exemple ce qu’on obtient en prenant les sommes des entiers de 1 à n comme premier et dernier terme de la n-ième ligne, après le sommet 0.
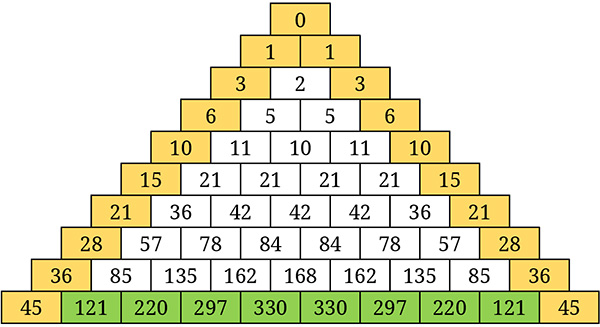
La somme des cases de la ligne n vaut 2(2n – n – 1) et donc pour la neuvième ligne, la somme vaut 2026.
2026 dans la suite de Kolakoski
Regardons la suite de 1 et de 2 qui commence par :
1221121221221121122121121221…
Lorsqu’on note le nombre de 1 ou 2 qui se suivent, on trouve d’abord un 1, puis deux 2, deux 1, un 2, un 1, etc. La suite des longueurs des plages de valeurs identiques successives est 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2… On retombe sur la même suite !

En partant d’un 1, il n’y a qu’une seule suite qui vérifie cette propriété, dite suite de Kolakoski, du nom de William Kolakoski (1944-1997), artiste et amateur de récréations mathématiques américain. Beaucoup de conjectures restent aujourd’hui ouvertes au sujet de cette suite, notamment des questions concernant ses plages de chiffres consécutifs. On en compte, par exemple, quatre de longueur 2 : 11, 12, 21 et 22. Il y en a six de longueur 3 : 112, 121, 122, 211, 212 et 221 (il n’y a pas de 111 ni de 222). Et des plages de longueur 47, combien y en a-t-il ? Eh oui, 2026.
Au piquet !
Pour finir ce tour d’horizon consacré à 2026, intéressons-nous aux tours de Hanoï. Ce fameux casse-tête inventé par l’espiègle Édouard Lucas (1842-1891) en 1889 est constitué de trois piquets. Le premier piquet contient une pile d’anneaux de taille décroissante qu’il s’agit de déplacer sur le troisième piquet en respectant les règles suivantes : ne jamais saisir plus d’un seul anneau à la fois et ne jamais disposer un plus grand anneau sur un plus petit. Le jeu est bien connu de tous les amateurs et amatrices de récréations mathématiques et il faut 2n – 1 coups au minimum pour déplacer n anneaux. Au-delà de sa résolution, le jeu renferme des trésors insoupçonnés au premier abord. Beaucoup de variantes ont été proposées depuis (voir Itération et récurence, Bibliothèque Tangente n°76, POLE, 2021) et certaines questions restent encore ouvertes aujourd’hui !
Mais connaissez-vous la variante « magnétique » inventée par l’Israélien Uri Levy ? Dans cette version, les anneaux ont deux faces (disons une bleue, une rouge) qu’on peut imaginer polarisées comme des aimants. Comme dans le jeu classique, on ne peut déplacer qu’un seul anneau à la fois mais on doit en plus le retourner avant de le reposer et, bien sûr, comme les anneaux sont aimantés, on ne peut pas se faire toucher deux faces de la même couleur.
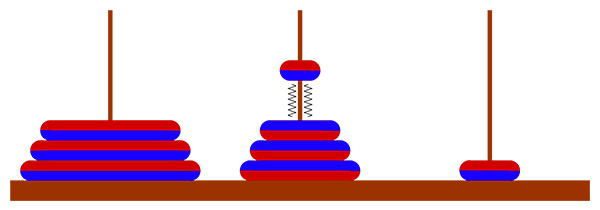
Dans les tours de Hanoï magnétique il faut retourner les anneaux
à chaque coup et tenir compte de la polarisation.
Pour la pile de deux anneaux, il faut donc maintenant 4 mouvements au minimum pour résoudre le casse-tête (contre 3 pour le jeu classique). Les tours de Hanoï les plus fréquentes possédent huit anneaux et il faut alors 255 mouvements pour résoudre le casse-tête. Dans la version magnétique, avec huit anneaux, on passe à 2026 mouvements !
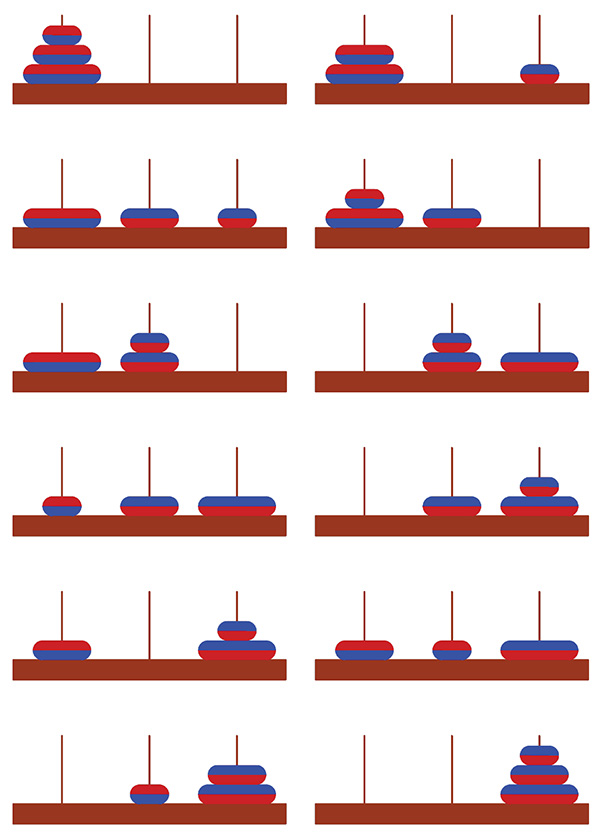
Avec 3 anneaux, il faut au moins 11 mouvements
pour résoudre les tours de Hanoï magnétiques.
2026, une année heureuse ?
Il est peut-être trop tôt pour le dire… Mais, par contre 2026 est un nombre heureux, contrairement à 2025 ! En effet (voir l'article « Il en faut peu pour être heureux »), si on additionne les carrés de ses chiffres et si on recommence ce processus, on finit par tomber sur 1. Les résultats successifs sont 22 + 02 + 22 + 62 = 44, 42 + 42 = 32, 32 + 22 = 13, 12 + 32 = 10 et 12 + 02 = 1. Il a fallu cinq étapes pour montrer que 2026 appartient à cette famille d’entiers, très minoritaires puisque sans doute moins de 20 % d’entre eux y appartiennent. On espère que ce n’est pas le cas des années…
Alors, qui a dit que l’année 2026 ne serait mathématiquement pas aussi intéressante que la précédente ? Avec cet aperçu certainement non exhaustif, voilà de quoi se convaincre du contraire pour bien débuter l’année !
