L’un des plus anciens problèmes des mathématiques est celui de la quadrature du cercle : construire un carré ayant même aire que l’intérieur d’un cercle. Un autre problème célèbre est celui de la duplication du cube. À chaque fois, il s’agit de construire, à la règle et au compas, un nombre donné : π ou .
Une question naturelle est alors : quels sont les nombres que l’on peut « construire à la règle et au compas » ? La réponse a été donnée seulement au XIXe siècle.
Un peu d’histoire
Qu’est-ce qu’un nombre ? Dans l’Antiquité, on confondait nombre et mesure. Par conséquent, des difficultés étaient présentes : comment définir le « produit » de deux nombres ? Si l’on représente le produit de deux nombres (mesures), on obtient une aire, un volume pour le produit de trois nombres, et… quelque chose de bizarre si l’on multiplie deux aires ! Quant au quotient de deux nombres, ce peut être une mesure (le quotient d’une aire par une longueur), ou un nombre sans dimension si les deux nombres sont des longueurs.
Il faut attendre René Descartes et sa fameuse Géométrie en 1637 pour que le nombre soit introduit en géométrie, avec une idée toute simple mais géniale : le mathématicien et philosophe français choisit un segment qu’il pose de longueur 1, et il rapporte ensuite les mesures (longueurs, aires, volumes…) à cette mesure-étalon. Ainsi, « construire » un nombre, c’est construire un segment ayant pour longueur ce nombre. Puis Descartes, presque subrepticement, introduit les coordonnées appelées maintenant cartésiennes pour « représenter algébriquement » un point du plan en utilisant deux nombres.

Une question naturelle se pose alors : quels sont les points que l’on peut construire en utilisant un nombre fini de fois les outils de base de la géométrie, à savoir une règle non graduée et un compas ? Et par voie de conséquence, quels sont les nombres « constructibles » ?
Avec une règle et un compas
Les deux constructions de base que l’on peut faire avec la règle (non graduée) et le compas, deux outils utilisés depuis l’Antiquité, sont les tracés de :
• la droite passant par deux points distincts ;
• le cercle de centre un point et passant par un autre point.
À partir de ces deux-là, en les combinant, on peut construire :
• la perpendiculaire à une droite (donnée par deux points) passant par un point ;
• la parallèle à une droite (donnée par deux points) passant par un point ;
• la médiatrice d’un segment déterminé par deux points et donc le milieu de ce segment ;
• la bissectrice d’un angle déterminé par deux demi-droites de sommet un point ;
• le symétrique d’un point par rapport à un autre ;
• le report d’une longueur donnée…
Par contre, avec ces outils, les Grecs n’ont pas su résoudre certains problèmes : la quadrature du cercle ou la duplication du cube, par exemple. Depuis les travaux de Pierre-Laurent Wantzel, on sait pourquoi !
On se place dans le plan et on choisit deux points O et I. Un point du plan est alors constructible s’il peut être obtenu comme intersection de deux objets obtenus par une succession de constructions géométriques (voir encadré), employant uniquement la règle non graduée et le compas, appliquées aux deux points de base O et I.
Tout d’abord, on trace la droite passant par ces deux points, puis on construit la perpendiculaire à la droite (OI ) passant par O. Sur cette perpendiculaire, on place le point J tel que les segments [OI ] et [OJ ] aient même longueur. On a alors un repère orthonormé.
Un nombre est alors dit constructible si c’est l’abscisse (ou l’ordonnée) d’un point constructible. En conséquence, quand un point est constructible, ses deux coordonnées sont des nombres constructibles… et réciproquement.
L’abscisse du point I étant égale à 1, le nombre 1 est constructible. En reportant la longueur OI un certain nombre de fois à partir de I, on en déduit que tous les entiers positifs sont constructibles ; il en va de même pour les entiers négatifs en reportant à partir de O. La construction du symétrique d’un point de la droite (OI ), d’abscisse x, par rapport à O montre que si x est constructible, alors ‒x l’est aussi.
On considère maintenant deux nombres x et y positifs et constructibles. Soient M le point de l’axe (OI ) d’abscisse x et N le point d’ordonnée y sur l’axe (OJ ). On construit le point P sur l’axe (OI ) tel que MP = ON : on en déduit que x + y = OP est constructible.
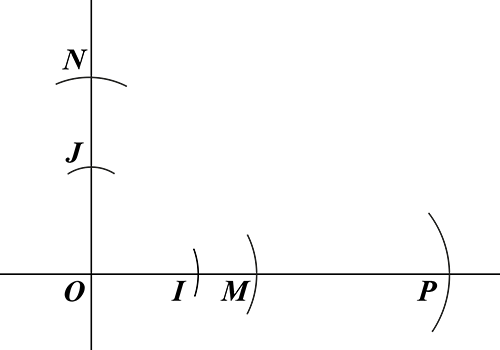
OP = OM + ON avec ON = MP.
M et N étant toujours les points de coordonnées (x, 0) et (0, y), on construit (à la règle et au compas) le point P de l’axe (OJ ) tel que [IN] soit parallèle à [MP]. En appliquant le théorème de Thalès, on obtient : OI / OM = ON / OP, d’où OP = OM × ON car OI = 1. Le nombre xy est donc constructible.
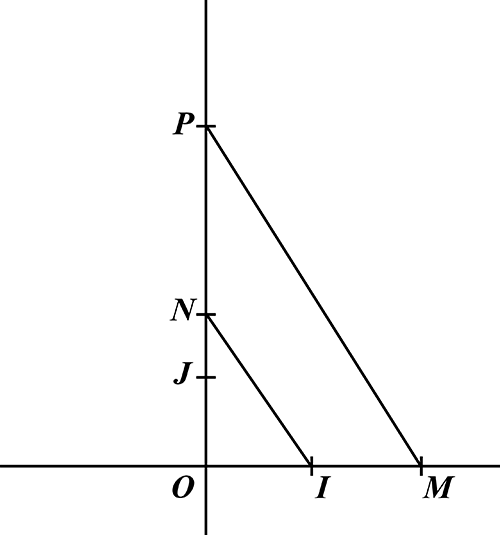
En utilisant la même figure, si maintenant on suppose que ce sont M et P qui sont constructibles, on a toujours ON = OP / OM et donc le quotient de deux nombres constructibles est aussi constructible.
Ainsi, si x et y sont deux nombres constructibles réels, les nombres x + y, xy et x/y sont constructibles. L’ensemble C des nombres constructibles (à ne pas confondre avec l’ensemble ℂ des nombres complexes) étant contenu dans l’ensemble ℝ des nombres réels, ces opérations possèdent les propriétés habituelles : C, muni de l’addition et de la multiplication, est un corps, tout comme ℝ et ℂ.
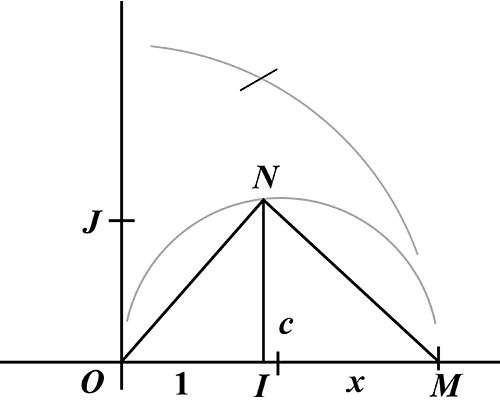
Montrons maintenant que si x est positif et constructible, alors est aussi constructible. Sur l’axe (OI ), construisons le point M tel que IM = x. Puis construisons le cercle de diamètre [OM ] et soit N son intersection avec la perpendiculaire à (OI ) en I.
Le triangle OMN est donc rectangle en N et de hauteur [IN]. On a IN2 = OI × IM, d’où IN2 = x et
L’ensemble des nombres constructibles est stable par la racine carrée des nombres positifs. C’est en fait le plus petit corps contenant le corps ℚ des rationnels et stable par racine carrée.
Les corps interviennent
Un nombre constructible est obtenu comme abscisse (ou ordonnée) d’un point construit, à chaque étape, par intersection de droites ou de cercles définis à l’étape précédente. Comment cela se traduit-il en termes d’algèbre ?
Notons P l’ensemble des points constructibles obtenus à une certaine étape et K l’ensemble des nombres constructibles correspondants. Par des arguments similaires à ceux employés précédemment, K est stable par addition, multiplication et division : c’est un corps. De plus, les coefficients de l’équation d’une droite passant par deux points de P appartiennent à K. Il en est de même pour l’équation d’un cercle de centre un point de P et passant par un point de P.
À ce stade, un nouveau point peut être obtenu de trois manières différentes :
1. Comme intersection de deux droites passant par des points de P ;
2. Comme intersection d’une droite passant par deux points de P et d’un cercle de centre un point de P et passant par un point de P ;
3. Comme intersection de deux cercles, chacun de centre un point de P et passant par un point de P.
Dans le premier cas, les coordonnées du nouveau point doivent vérifier les deux équations de droites : ce sont donc les solutions d’un système de deux équations du premier degré. Elles s’expriment comme somme, produit et quotient des coefficients des équations des deux droites, donc appartiennent toujours à K.
Dans le deuxième cas, les coordonnées du nouveau point doivent vérifier une équation du premier degré (l’équation de la droite) et une équation du second degré (celle du cercle), les divers coefficients appartenant tous à K. En exprimant l’une des inconnues, par exemple y, en fonction de l’autre, c’est-à-dire ici x, dans la première équation et en reportant dans la deuxième, on obtient que x est solution d’une équation du second degré avec des coefficients appartenant à K. Son discriminant Δ (le fameux b 2 ‒ 4ac) appartient à K : les deux solutions s’écrivent sous la forme α et β appartenant aussi à K. Elles appartiennent donc à
extension quadratique (voir encadré) de l’ensemble K.
Dans le dernier cas, on se ramène au cas précédent en éliminant les termes de degré 2 dans l’une des équations : pour cela, il suffit de la remplacer par la différence des deux équations.
Ainsi, dans tous les cas, si les nombres constructibles à une certaine étape appartiennent à un corps K, alors il existe un élément Δ positif appartenant aussi à K tel que les nombres constructibles à l’étape suivante appartiennent à extension quadratique de l’ensemble K des nombres constructibles de l’étape précédente.
Ce phénomène se reproduit à chaque étape de la construction. Or, au départ K0 = ℚ. On peut en conclure qu’un nombre réel x est constructible à la règle et au compas s’il existe (et la condition est suffisante) une suite finie Kn, pour n variant de 0 à r, de sous-corps de ℝ tels que :
• K0 = ℚ ;
• K0 ⊂ K1 ⊂ … ⊂ Kn ⊂ … ⊂ Kr où Kn est une extension quadratique de Kn‒1 pour n > 0. Cela signifie qu’il existe dn‒1 appartenant à Kn‒1 (et qui n’est pas un carré) tel que
• x appartient à Kr .
Cette suite d’extensions quadratiques porte quelquefois le nom de tour d’extensions quadratiques.
Un nouveau corps
Soit K un sous-ensemble de nombres réels stable par addition et multiplication et contenant l’opposé et l’inverse de chacun de ses éléments (non nul pour la division) : autrement dit, muni de ces opérations, c’est un sous-corps de ℝ.
Si d est un élément de K, avec d > 0, l’ensemble des éléments qui s’écrivent avec a et b appartenant à K, est aussi un sous-corps de ℝ. On laisse le lecteur s’en convaincre (en s’inspirant éventuellement de l’article « L'esprit de corps quadratique »). Ce sous-corps, qui contient K, est noté
Il peut éventuellement être égal à K si d est un carré ! Si ce n’est pas le cas, on dit que c’est une extension quadratique de K.
Si appartient à
son conjugué, souvent noté
, est défini par
Les relations suivantes sont faciles à vérifier : et
appartiennent à K, ainsi que
si
ce qui est plus surprenant ! On retrouve là la notion de conjugué dans l’ensemble ℂ des nombres complexes, qui n’est rien d’autre que
Dans le cas où K = ℚ, l’ensemble des nombres rationnels, on peut remarquer que est égal à
En effet, on a l’égalité
Tout constructible est algébrique
On va montrer que si x est constructible, il est racine d’une équation polynomiale à coefficients rationnels (donc à coefficients entiers en multipliant par un entier « bien choisi », par exemple le plus petit commun multiple de tous les dénominateurs) : c’est donc un nombre algébrique. Et le degré de cette équation est une puissance de 2, car x est obtenu par une succession d’extensions quadratiques de ℚ, comme on vient de le voir.
En effet, à chaque étape de la construction, si K est un corps et si L est une extension quadratique de K, c’est-à-dire si où d est un nombre positif de K qui n’est pas un carré dans K, alors tout nombre de L est racine d’un polynôme de degré 2 à coefficients dans K : en effet, le nombre
avec a et b dans K, vérifie l’équation
(X ‒ a) 2 = b 2 d.
Si, maintenant, on considère M, une extension quadratique de L vérifiant donc où d’ est un nombre positif de L qui, lui-même, n’est pas un carré. Tout nombre x de M est racine d’un polynôme de degré 2 à coefficients dans L, comme ci-dessus. On a donc X 2 + uX + v = 0, où u et v sont des nombres de L. On considère alors l’équation
où
et
sont les conjugués de u et v dans L (voir encadré).
Alors x est aussi racine de l’équation de degré 4 obtenue en faisant le produit de ces deux équations Or, en développant cette équation, on obtient :
On peut alors constater (voir encadré) que tous les coefficients de ce polynôme appartiennent à K ! Le nombre x appartenant à M est non seulement racine d’un polynôme de degré 2 à coefficients dans L, mais aussi racine d’un polynôme de degré
4 = 22 à coefficients dans K.
On devine ainsi comment, en descendant la suite des extensions quadratiques jusqu’à K0 = ℚ, on montre que tout nombre constructible est algébrique, et est racine d’une équation de degré 2r, obtenue par cette succession.
Maintenant il est possible de donner des réponses aux problèmes de l’Antiquité :
• la quadrature du cercle est impossible puisque π est transcendant (voir article « Un nombre qui dépasse la raison », donc non algébrique, encore moins constructible ;
• la duplication du cube est impossible puisque n’est pas constructible (le polynôme de degré minimal dont il est racine est de degré 3 : il s’agit de X 3 ‒ 2 ; et il est facile de vérifier que
n’est pas racine d’un polynôme de degré 2), bien qu’il soit algébrique.
Mais la condition obtenue sur le degré du polynôme n’est qu’une condition nécessaire. La réciproque n’est pas vraie : un nombre algébrique de degré une puissance de 2 (c’est-à-dire tel que le polynôme de plus bas degré dont il est racine soit de degré une puissance de 2) n’est pas obligatoirement un nombre constructible. L’exemple le plus connu, mais pas très simple, est celui des racines du polynôme X 4 ‒ X ‒ 1 : ces dernières sont bien de degré 4, mais elles s’expriment à l’aide de (!). Par conséquent, nécessitant une racine cubique, ce ne sont pas des nombres constructibles.
Toute cette théorie, proprement algébrique, a été mise en place principalement par Pierre-Laurent Wantzel dans un article publié en 1837 dans Le Journal de mathématiques pures et appliquées de Joseph Liouville. Malheureusement, il semble que ce travail soit demeuré un peu oublié jusqu’aux années 1930 et n’ait pas participé pleinement à la percée de l’algèbre dans toute la mathématique, contrairement à la théorie de Galois.
Pierre-Laurent Wantzel
Fils d’un ancien militaire devenu professeur de mathématiques, très jeune, il s’intéresse à cette discipline. Reçu premier à l’École polytechnique à l’âge de 18 ans, il intègre ensuite l’École des ponts et chaussées en 1834. C’est en 1837, alors qu’il est encore élève-ingénieur, qu’il publie ses travaux sur les nombres constructibles. Quelques années plus tard, il publie une démonstration du théorème d’Abel sur les équations résolubles par radicaux, plus simple que l’originale.
Ingénieur des ponts et chaussées, il préfère se consacrer à l’enseignement. À son décès, on a pu lire, dans les Nouvelles Annales de Mathématiques, un long article biographique commençant par : « Les sciences mathématiques viennent de perdre, avant qu’il eût atteint trente-quatre ans, un des hommes sur lesquelles elles pouvaient fonder les plus belles espérances. » Mais il n’a sans doute pas eu la notoriété qu’il aurait méritée.

Pierre-Laurent Wantzel (1814‒1848).


