
Tout le monde a entendu parler de l’espace dit euclidien, ensemble de points dans lequel nous pratiquons la géométrie depuis que les notions de repères et de coordonnées ont été offertes au monde mathématique. Avec quelques aménagements, et un effort de modélisation de la réalité, la dimension 3 correspond pratiquement à ce que nous pouvons percevoir de l’environnement dans lequel nous évoluons, quand la dimension 2 est le plan des représentations, du tableau à la page de cahier.
L’espace dans tous ses états
La notion abstraite d’espace mathématique recouvre pourtant une conception bien différente de ce que nous dicte notre intuition. Sa conceptualisation traduit la volonté de classifier et cartographier les savoirs, mais également, dans un souci d’universalité, de regrouper des idées similaires. Un espace est, en effet, une sorte d’ « environnement de travail » pour le mathématicien, que l’on obtient en équipant un ensemble d’une structure (une « boîte à outils ») qui peut être issue de l’algèbre, de l’analyse voire de la géométrie.
Les raisonnements et les calculs usuels (par exemple, sur les réels) effectués avec une structure donnée resteront valables même si on change l’objet d’étude. On pourra ainsi dupliquer ces techniques sur les ensembles de nombres, de vecteurs, de fonctions… ou même d’ensembles.
Un ensemble E, s’il est muni d’une structure algébrique (opérations + et ∙ vérifiant certaines conditions), devient un espace vectoriel sur lequel on peut faire des raisonnements algébriques et géométriques. Si le même ensemble est muni d’une structure topologique, il devient un espace topologique et on se plonge alors dans l’analyse (limites, continuité de fonction, convergence de suites…).
De même, l’ensemble E sera un espace mesurable si on l’équipe d’une structure appelée tribu. Il se peut, dans certains domaines et selon les besoins pratiques, que l’on équipe un ensemble de deux ou plusieurs structures (en respectant une harmonie entre ces structures). On obtient ainsi, par exemple, un espace vectoriel topologique ou un espace topologique mesurable.
Les espaces topologiques
Pour pratiquer l’analyse, on définit les limites, la convergence et la continuité à partir d’axiomes et de règles, que l’on appelle une topologie (voir en encadré ci-desssous).
Définir une topologie
Une topologie sur un espace E est un ensemble de parties de E (appelées ouverts) qui vérifient les trois axiomes :
→ l’ensemble entier est un ouvert (l’ensemble vide ∅ aussi) ;
→ l’union finie ou infinie d’ouverts est un ouvert ;
→ l’intersection finie d’ouverts est un ouvert.
On peut trouver plusieurs topologies sur un même ensemble.
L’ensemble P(E), des parties de E, constitue une topologie sur E appelée topologie discrète.
L’ensemble T = {∅, E} est une topologie sur E appelée topologie grossière.
Sur ℝ, une topologie est, par exemple, constituée des intervalles ouverts et l’union de tels intervalles. C’est la topologie usuelle.
Par exemple, en considérant ℝ comme un espace topologique, on définit la convergence de la façon suivante.
Dans ℝ, une suite (un) converge vers un nombre réel a si et seulement si pour tout intervalle ouvert I contenant a, les termes de la suite (un) appartiennent à I à partir d’un certain rang p.
Plus généralement, sur un ensemble E, muni d’une topologie, la convergence d’une suite se définit de la même manière.
Une suite (un) converge vers un élément a si et seulement si pour tout ouvert O contenant a, les termes de la suite (un) appartiennent à O à partir d’un certain rang p.
Avec cette définition, on constate que la suite (1/n) n > 0 est bien convergente vers 0 dans ℝ muni de la topologie usuelle. Par contre, si ℝ est muni de la topologie discrète, la même suite n’est plus convergente. En effet, l’ensemble {0} est alors un ouvert pour la topologie discrète contenant le nombre 0 et il ne contiendra jamais aucun terme de la suite (1/n).
Par ailleurs, si l’on considère ℝ muni de la topologie grossière, toutes les suites d’éléments de ℝ sont convergentes (vers tout élément de ℝ !). On laisse le lecteur s’en convaincre.
Le rôle de la distance
En ajoutant une distance entre deux éléments, c’est-à-dire la possibilité de mesurer l’éloignement (par un réel positif), on se retrouve dans un espace métrique. À partir de cette distance, une topologie particulière est définie. Actualisons notre définition de la convergence.
Une suite (un) converge vers a si et seulement si pour tout nombre réel positif ε aussi petit que l’on veut, la distance entre un et a est plus petite que ε à partir d’un certain rang p.
Voici, par exemple, deux distances qui permettent de faire de ℝ un espace métrique :
• la distance habituelle entre deux réels x et y : d(x, y) = |x – y| ;
• la distance discrète définie par d(x, y) = 1 si x ≠ y et d(x, x) = 0.
On vérifiera que la suite (1/n)n > 0 converge bien pour la distance usuelle mais pas pour la distance discrète.
Dans un espace métrique, on rencontre les suites de Cauchy, suites dans lesquelles les éléments sont de plus en plus proches. Elles ne sont, pour autant, pas obligatoirement convergentes : il faut, pour cela s’assurer que si elles se rapprochent, elles se rapprochent bien de quelque chose, c’est-à-dire que la limite se trouve bien dans l’ensemble considéré, ou encore, de manière imagée, s’assurer que notre espace n’a pas de « trous ». Ce sera le cas pour les espaces métriques complets dans lesquels, donc, toutes les suites de Cauchy convergent (vers quelque chose !).
Ainsi ℝ* (muni de la distance usuelle) est bien un espace métrique mais il n’est pas complet. Par exemple, un = (-1)n/n (pour changer !) définit une suite de Cauchy qui ne converge pas (elle se rapproche de 0 qui n’est pas dans l’espace considéré).
L’ensemble ℚ avec la distance usuelle est un exemple classique d’espace métrique qui n’est pas complet : une suite de nombres rationnels peut s’approcher d’un réel, par exemple ou π.
L’algèbre s’invite
Avec les espaces vectoriels, on revient en terrain connu. On rappelle qu’un ensemble est un espace vectoriel s’il est muni de deux opérations (+ et ∙) qui permettent de réaliser des combinaisons linéaires entre les éléments. Par exemple, à partir des vecteurs u et v, on peut définir w = 3∙u + 2∙v (lequel est souvent noté 3u + 2v, c’est-à-dire sans le signe de l’opération ∙). Ces espaces, ainsi nommés par analogie avec les espaces de vecteurs que l’on rencontre en physique (on pourra vérifier, en examinant toutes les propriétés en encadré, que ce sont bien des espaces vectoriels sur l’ensemble des nombres réels), peuvent représenter une multitude d’ensembles d’objets mathématiques.
Définir un espace vectoriel
Pour qu’un ensemble muni de deux opérations (+ et ∙) soit un espace vectoriel (sur un corps K ) il faut, principalement :
• que l’opération interne + (addition de deux éléments de l’ensemble)
- soit associative : (a + b) + c = a + (b + c) ;
- commutative : a + b = b + a ;
- possède un élément neutre : a + 0 = a ;
- que tout élément possède un opposé : a + (-a) = 0 ;
• que l’opération ∙ (multiplication d’un élément de K et d’un élément de l’ensemble) vérifie k ∙ (a + b) = k ∙ a + k ∙ b.
k est généralement un nombre réel ou complexe. Négliger de s’intéresser à la nature de ce fameux corps K serait une erreur. Considérons, par exemple, l’ensemble ℂ des nombres complexes. ℂ est un espace vectoriel sur ℝ. À ce titre, il est de dimension 2 puisque tout nombre complexe a + ib peut s’exprimer comme combinaison linéaire des deux éléments : 1 et i.
Mais on pourrait également le considérer comme espace vectoriel sur le corps ℂ. Tout nombre complexe est le produit d’un complexe (élément du corps K ) et du vecteur de base : 1 (élément de l’espace ℂ). Et notre espace ℂ se retrouve être, dans ce cas, de dimension 1.
Ainsi, beaucoup d’ensembles ont des structures d’espaces vectoriels.
Dans un espace vectoriel, on rencontre les concepts de base et de dimension : une base est un ensemble minimal de vecteurs permettant d'exprimer tous les autres par combinaison linéaire. Ce nombre minimal de vecteurs est la dimension de l’espace.
Par exemple, l’espace ℝ2 des vecteurs de coordonnés (x ; y) est de dimension 2. Tous les éléments peuvent s’écrire en fonction de (1 ; 0) et (0 ; 1). De même, l’espace ℝ3 est de dimension 3.
L’espace des polynômes de degré inférieur ou égal à 3 est un espace vectoriel de dimension 4. La base canonique (1, x, x 2, x 3 ) est une des bases possibles de cet espace.
L’ensemble de toutes les fonctions continues sur [0 ; 1] est un espace vectoriel. Il n’est pas de dimension finie. On ne peut en effet pas trouver un nombre fini de fonctions qui engendrerait toutes les autres par combinaison linéaire.

Deux structures
En réunissant plusieurs de ces notions, on peut créer d’autres espaces.
Dans un espace vectoriel, on peut ainsi définir la notion de norme, nombre réel positif associé aux vecteurs de l’espace, représentant en quelque sorte leur longueur, ce qui permettra de définir la notion de limite et d’introduire les concepts de l’analyse.
Dans ce cas, la distance entre deux éléments a et b de l’ensemble est d(a,b) = ||b – a|| (où ||u|| est la notation pour la norme de u).
Par exemple, sur ℝ3, on peut définir plusieurs normes pour un vecteur x de coordonnées (x1 ; x2 ; x3) :
||x||1= |x1| + |x2| + |x3| ;
||x||∞ = max{|x1|,|x2|,|x3|}.
Ce qui est remarquable, c’est que ces trois normes sont équivalentes : si une suite de points tend vers (0 ; 0 ; 0) pour une norme, cela est vrai aussi pour une autre norme. Sur ℝ3, c’est vrai d’ailleurs pour deux normes quelconques. Cette propriété d’équivalence des normes est vraie pour tout espace de dimension finie.
On peut ainsi reprendre notre définition de la convergence dans le cas des espaces vectoriels normés.
Une suite (un ) converge vers a si et seulement si pour tout nombre réel positif ε aussi petit que l’on veut, on a ||un – a|| < ε à partir d’un certain rang p.
Revenons dans l’espace des fonctions continues sur l’intervalle [0 ; 1], et définissons, de la même manière des normes pour une fonction continue f :
Dans cet espace, toutes les normes ne sont pas forcément équivalentes (voir En Bref « Le monde des fonctions »).
Ainsi, certaines suites de fonctions peuvent converger pour certaines normes et pas pour d’autres.
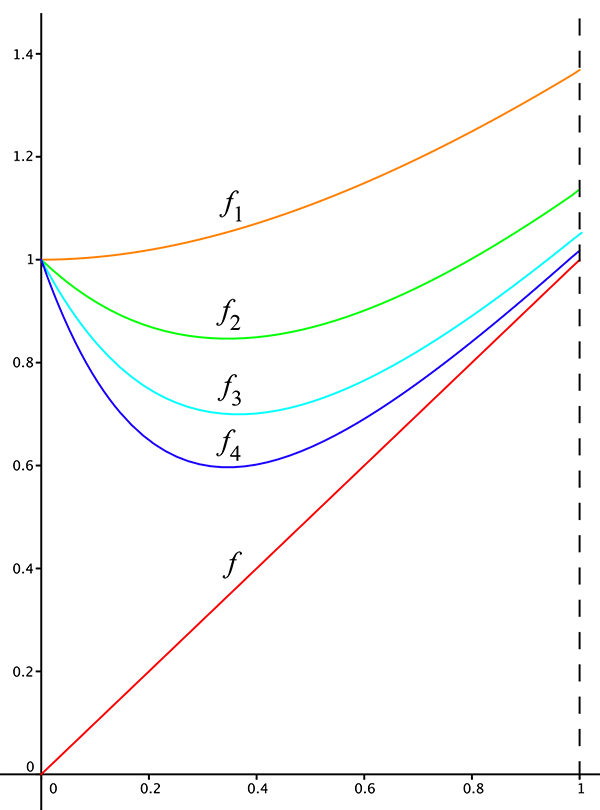
La suite de fonctions définie par fn(x) = x + e–nx, n > 0
converge vers f (x) = x pour les normes ||.||1 et ||.||2 mais pas pour ||.||∞.
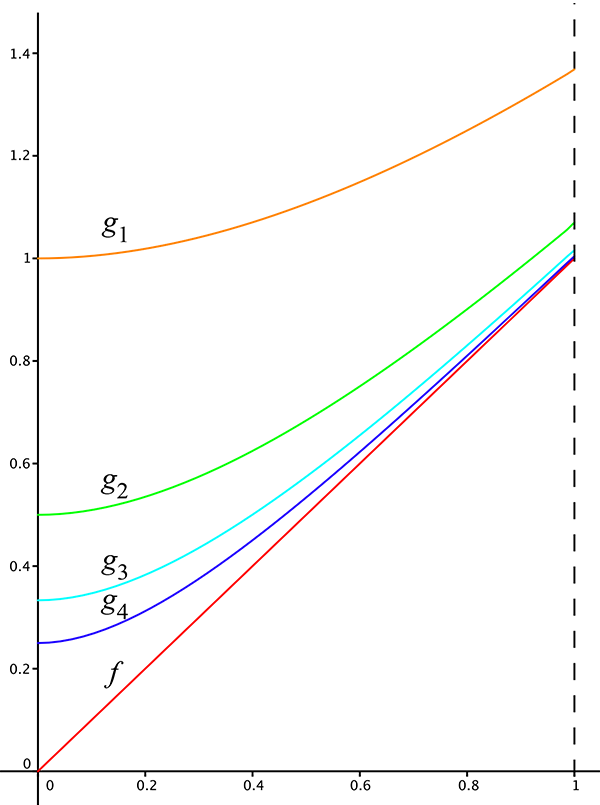
La suite définie par gn = x + e–nx / n,
pour n > 1converge vers f pour toutes les normes.
Les espaces vectoriels normés complets sont nommés espaces de Banach.
En plus des propriétés topologiques des applications (limites, continuité), les espaces de Banach nous offrent la possibilité de définir la notion de différentiabilité.
Tout faire avec le produit scalaire
Le produit scalaire est une autre manière de rendre compte d’un écart entre deux éléments d’un espace vectoriel. Dans notre espace habituel de vecteurs, il mesure l’angle entre deux vecteurs. S’il est nul, les deux vecteurs sont orthogonaux. Cette notion va permettre de réaliser des projections orthogonales et de résoudre des problèmes d’optimisation.
À partir du moment où l’on sait définir un produit scalaire sur un espace, il en découle une norme particulière, la norme euclidienne : (où < u,v > est la notation pour le produit scalaire de u et v).
Les normes ||.||2 des exemples précédents sont des normes euclidiennes. Les produits scalaires associés sont :
< u,v > = u1v1 + u2v2 + u3v3
Un espace de Hilbert est un espace vectoriel muni d’un produit scalaire, qui de plus est complet (voir En Bref « Le monde des fonctions ») pour la topologie induite par la norme hilbertienne . C’est donc un cas particulier d’espace de Banach.
Les espaces euclidiens sont des espaces de Hilbert de dimension finie. Il en est ainsi des espaces ℝn ou des espaces de polynômes de degré inférieur ou égal à n.
La mesurabilité
On sait mesurer des distances entre deux éléments, la « longueur » d’un élément ou l’ « angle » entre deux éléments, on va maintenant s’intéresser à la mesure d’une partie de l’espace.
La tribu (voir en encadré) est la structure qui rend un espace mesurable.
Pour faire partie de la tribu
Une tribu sur un espace E est un ensemble de parties de E qui vérifient les trois axiomes :
1- L’ensemble entier appartient à la tribu (ainsi que l’ensemble vide) ;
2- Le complémentaire d’un ensemble de la tribu appartient aussi à la tribu ;
3- L’union, finie ou dénombrable, d’une suite d’ensembles de la tribu appartient aussi à la tribu.
On définit une mesure en associant un réel positif à chaque élément de la tribu.
La mesure vérifie la propriété : mes (A ∪ B) = mes A + mes B, si A et B sont disjoints. Plus généralement la mesure d’une réunion finie ou dénombrable d’ensembles disjoints est la somme (ou la série) des mesures de chaque ensemble.
On montre alors, en particulier, que mes (A ∪ B) = mes A + mes B – mes (A ∩ B).
Un ensemble muni d’une tribu et d’une mesure est appelé un espace mesurable.
En voici quelques exemples.
Dans un espace probabilisé (voir article « Structurer le hasard »), l’ensemble est l’univers des possibles, la tribu est l’ensemble des évènements et la mesure pour chaque événement est sa probabilité (un nombre compris entre 0 et 1).
ℝ est un espace mesurable en prenant pour tribu l’ensemble des intervalles et pour mesure de tout intervalle de la tribu la longueur de celui-ci.
Considérons un ensemble E discret fini, par exemple {0, … , n}, munissons-le de la tribu constituée de l’ensemble des parties de E. Et définissons comme mesure d’une partie le cardinal de cette dernière. C’est la mesure de comptage.
Soit E non vide avec pour tribu l’ensemble de ses parties. Pour un élément a de E, on définit la mesure suivante pour tout A dans la tribu :
mes A = 1 si a ∈ A ;
mes A = 0 si a ∉ A.
C’est la masse de Dirac relative à a.
Signalons encore, pour finir, que les ensembles dont la mesure est nulle sont appelés ensembles négligeables et que les espaces mesurables ont permis, entre autres, de mettre au point la notion d’intégrale.
L’outil de la mesure peut également constituer une manière de faire converger une fonction : il s’agit de la convergence presque partout (convergence sauf sur un ensemble négligeable).
Pour ceux qui se demanderaient comment, en pratique, le mathématicien use des espaces à sa disposition, en voici une illustration. Pour de nombreux problèmes (équations différentielles, équations aux dérivées partielles...) que l’on ne sait pas résoudre de manière exacte, on cherche à construire une suite d’approximations de la solution.
Le problème consiste souvent à trouver l’environnement (norme, produit scalaire, topologie...) adéquat pour montrer la convergence de cette suite vers la solution théorique.


