
Les fonctions s’étudient généralement dans des espaces vectoriels normés (voir article
« Des environnements pour le mathématicien »). On peut disposer de plusieurs normes. Mais, contrairement à ce qui se passe dans ℝn (et plus généralement lorsque la dimension est finie), les normes ne sont pas toujours équivalentes, au sens où elles ne préservent pas toujours les mêmes propriétés topologiques (convergence, continuité, complétion…). Il est donc toujours délicat de choisir une norme plutôt qu’une autre. Selon le problème posé (approximation par des fonctions polynomiales, résolution d’équations aux dérivées partielles…), on en choisira une qui soit adaptée à la technique utilisée. La norme || .|| 2 est assez souvent « gagnante » en raison du produit scalaire qui se cache derrière et donc de la possibilité d’utiliser les outils des espaces de Hilbert.
Convergence… ou pas
Voici quelques exemples de normes pour une fonction f dans l’espace des fonctions continues sur l’intervalle [0 ; 1] :
La notion de convergence dans cet espace vectoriel normé se définit par :
Une suite de fonctions (fn) converge vers f si et seulement si pour tout nombre réel positif ε aussi petit que l’on veut, on a||fn – f || < ε à partir d’un certain rang p.
Par exemple, pour la suite des fonctions définie par fn(x) = x + e–nx,
pour n > 0 et la fonction limite f(x) = x, un calcul simple nous donne
Comme cette quantité tend vers 0, on en déduit que cette suite converge vers la fonction f pour la norme ||.||1. De la même manière, il y a convergence pour la norme ||.||2.
Cependant, la suite ne converge pas vers f pour la norme ||.||∞.
En effet, pour tout n >1 on a : ||fn – f||∞ = max {e–nx, x ∈ [0,1]} = 1.
Considérons la suite définie par gn = x + e–nx/n, pour n > 1.
On a, dans ce cas : ||gn– f ||∞ = max { e–nx/n, x ∈ [0,1]} = 1/n.
On en conclut alors que la suite (gn) converge pour la norme ||.||∞.
Cette convergence (pour la norme ||.||∞) est appelée convergence uniforme. Sur cet espace, elle implique la convergence pour les normes ||.||1 et ||.||2.
Complet ou pas complet ?
Un espace est dit complet si toute suite de Cauchy y est convergente (voir article « Des environnements pour le mathématicien »).
La norme joue, ici aussi, un rôle important.
Retournons dans notre espace des fonctions continues sur [0 ; 1] et intéressons nous aux fonctions hn définies, pour n > 1, de la façon suivante :
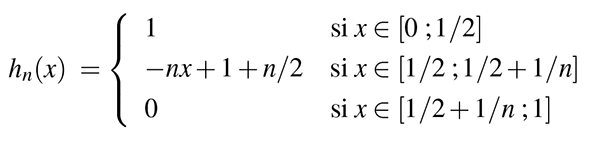
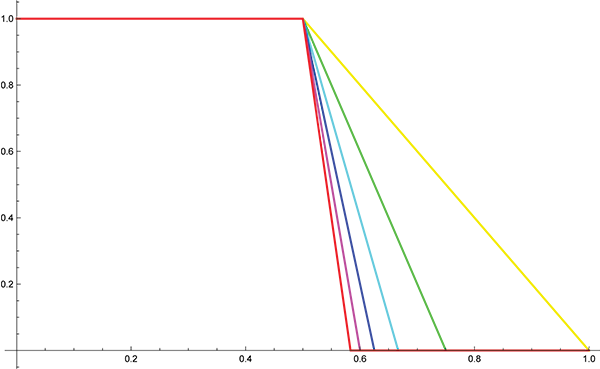
Les fonctions hn pour n = 2, 4, 6, 8, 10, 12.
Pour des entiers n et p > 2 les calculs montrent que : ||hn + p – hn||1 = p/2n (n + p).
Cette égalité indique que, pour tout nombre réel positif ε (aussi petit que l’on veut), on peut trouver un nombre n tel que ||hn + p – hn||1 < ε. La suite (hn) est donc une suite de Cauchy.
La limite plausible de cette suite est une fonction h qui vaut 1 sur [0 ; 1/2[ et 0 sur l’intervalle [1/2 ; 1]. On vérifie, d’ailleurs, que la quantité ||hn – h||1 =1/2n tend vers 0. Cependant la fonction h n’est pas continue ! Donc, elle n’appartient pas à notre espace. Par conséquent, la suite (hn), qui est pourtant une suite de Cauchy, ne converge pas dans cet espace.
On en déduit alors que l’espace des fonctions continues sur [0 ;1] n’est pas complet pour la norme ||.||1. Par contre, on peut montrer qu’il est complet pour la norme ||.||∞.


