Le mathématicien indien Bhaskara II (1114–1185) explique dans son traité la Lilavati comment calculer le contenu d’une excavation en forme de tronc de pyramide dont les dimensions sont celles de la figure.
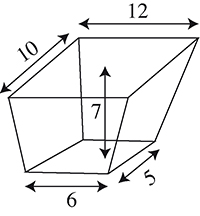
Bhaskara donne en toutes lettres sa méthode de calcul : « La somme des aires des bases et de l’aire d’un rectangle de largeur la somme des largeurs des bases et de longueur la somme des longueurs des bases étant divisée par 6 puis multipliée par la profondeur donne le volume. »
Calculez le volume de cette excavation par la méthode de Bhaskara, puis calculez le volume de ce tronc de pyramide en le considérant comme la différence des volumes de deux pyramides. Comparez les deux résultats.
D’une manière générale, on considère une excavation de profondeur h dont les dimensions de la grande base sont L et l et celles de la petite base, kL et kl (k étant un nombre réel compris entre 0 et 1).
Calculez le volume de cette excavation par les deux méthodes précédentes. La méthode de Bhaskara est-elle valable ?

