Anne et Bernard disposent de pièces en forme de S et de Z (elles ne peuvent pas être retournées recto verso) qu’ils peuvent placer sur un quadrillage régulier (chaque petit carré d’une pièce doit recouvrir exactement une case du quadrillage).
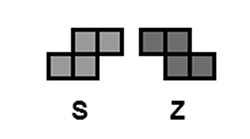
Bernard déclare : « Un calcul simple montre que l’on peut placer au plus vingt pièces dans un carré de neuf cases de côté. »
Anne précise : « Humm, c’est plus compliqué que ça ; en fait, on peut en placer au plus seize. »
Montrez qu’elle a raison.
Bernard dessine un polygone dont les côtés suivent les lignes du quadrillage. Anne réussit à le paver exclusivement avec des S. Après avoir enlevé tous les S placés par Anne, Bernard réussit à le paver avec des S et avec des Z.
Montrez qu’il a placé un nombre pair de Z.
Indices : pour la première question, il convient d’appliquer le principe des tiroirs sur des cases astucieusement choisies. La seconde question peut être résolue en introduisant deux couleurs et en appliquant l’arithmétique modulaire sur les coordonnées dans le plan.

