Le « haha », pour Martin Gardner (voir Tangente 136), est un éclair subit de l’esprit qui nous fait comprendre le ressort d’une situation mathématique ainsi qu’un raccourci permettant de résoudre le problème presque instantanément et… sans effort. Nous vous proposons ici quelques énigmes pour lesquelles Gardner préconise de trouver le bon « haha ».
1 – La girafe

Ces cinq allumettes représentent une girafe. Sauriez-vous, en ne déplaçant qu’une seule des allumettes, obtenir une autre position de la même girafe ?
Note : on ne tiendra pas compte de la position des embouts rouges des allumettes.
2 – La diagonale
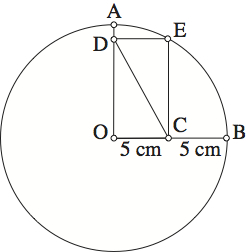
Un rectangle ODEC est inscrit dans un quart de cercle de centre O comme l’indique la figure. Pouvez-vous instantanément donner la longueur de la diagonale CD ?
3 – Les six pièces

À partir de la disposition de gauche, vous voulez obtenir la disposition de droite. Le seul mouvement autorisé est le suivant : vous devez faire « rouler » une pièce, celle-ci devant rester constamment en contact avec au moins une autre pièce, le mouvement ne pouvant prendre fin que dans une position où la pièce déplacée est en contact « rigide » avec deux autres pièces.
Réalisez cette transformation en trois mouvements.
La difficulté réside dans la pièce centrale. Si on la déplace en premier, on ne peut plus refermer la boucle, faute de pouvoir appuyer la dernière sur deux pièces…
4 – De huit à dix pièces et plus
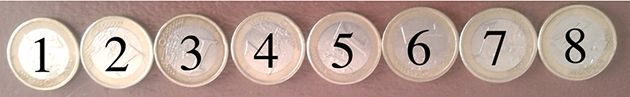
Vous devez empiler ces huit pièces en quatre piles de deux pièces en respectant la règle suivante. Une pièce seule peut sauter par-dessus deux pièces (qui peuvent être disposées côte à côte ou déjà empilées l’une sur l’autre) pour se poser sur une pièce seule contiguë aux deux pièces sautées.
Voici une solution : 4 va en 7, 6 passe en 2, on déplace 1 en 3, puis 5 en 8.
En respectant la même règle, sauriez-vous maintenant réaliser cinq piles de deux pièces à partir d’un alignement de dix pièces ?
Et comment procéderiez-vous pour 2n pièces (avec n > 5) ?
5 – Les quinze pions
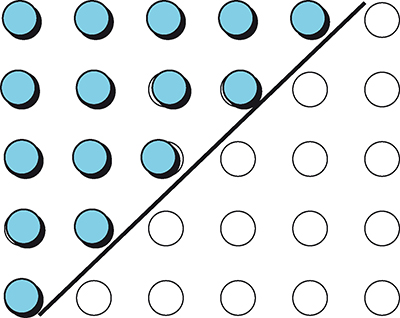
Sur un réseau 6 × 5, quinze pions sont disposés, comme le montre la figure, dans les quinze emplacements situés au-dessus et à gauche de la ligne oblique. Le but du jeu est de les déplacer dans les quinze emplacements vides en dessous et à droite de la ligne oblique, le seul mouvement autorisé étant le saut d’un pion par-dessus un autre pion pour se poser dans une case adjacente vide.
Est-il possible de transférer les quinze pions sous la ligne ?
6 – Les quatre punaises
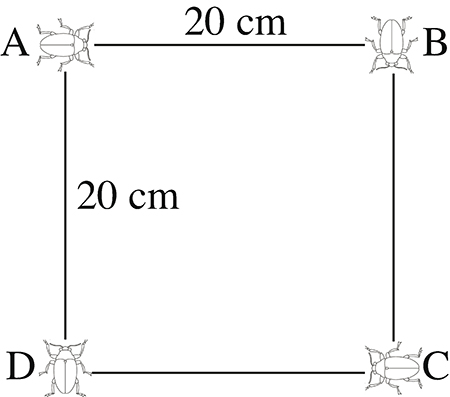
Les punaises A, B, C et D sont situées aux sommets d’un carré de 20 cm de côté. A et C sont des punaises mâles, B et D sont des femelles.
De façon simultanée, A se dirige directement en direction de B, B en direction de C, C en direction de D et D en direction de A. Si les quatre punaises se déplacent à une vitesse constante identique, elles vont décrire quatre spirales logarithmiques superposables qui se rencontreront au centre du carré.
De quelle distance chaque punaise s’est-elle déplacée depuis son point de départ ?
7 – Deux carrés qui se chevauchent
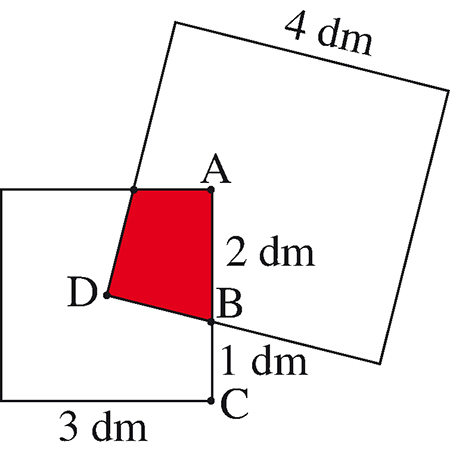
Deux carrés de côtés respectifs 3 dm et 4 dm se chevauchent, comme l’indique la figure, le sommet D du grand carré étant situé au centre du petit.
Quelle est la surface de la zone rouge ?
8 – Le banlieusard
Ce banlieusard a l’habitude d’arriver à sa station de banlieue chaque soir exactement à cinq heures. Sa femme vient le chercher au train et le ramène chez lui. Un jour, il prend un train plus tôt, arrivant à la station à quatre heures. Le temps est agréable, donc plutôt que de téléphoner à la maison, il commence à marcher le long de la route toujours habituellement prise par son épouse. Il la rencontre quelque part en chemin, monte dans la voiture, et ils rentrent chez eux, arrivant à leur domicile dix minutes plus tôt qu’à l’accoutumée.
En supposant que la femme conduit toujours à une vitesse constante, et qu’à cette occasion elle est partie juste à temps pour arriver au train de cinq heures, pouvez-vous déterminer combien de temps le mari a marché avant de monter en voiture ?
9 – Les six cavaliers
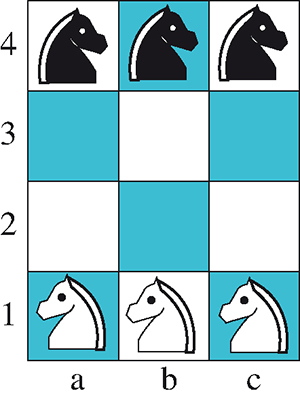
Il s’agit ici d’échanger les positions des cavaliers blancs et des cavaliers noirs en utilisant les déplacements standard des cavaliers d’échecs (déplacement vers une case libre selon la diagonale d’un rectangle de deux cases sur trois cases).
En 1974, lorsque ce problème a été publié dans le Journal of Recreational Mathematics, il a été considéré comme trivial avec une solution en vingt-six déplacements. Plus tard, une solution en dix-huit mouvements a été trouvée. Martin Gardner a inclus ce problème dans son recueil Aha! Insight ! (W.H. Freeman & co., 1978) en citant la solution en dix-huit coups comme la meilleure.
Depuis, un nombre de mouvements strictement inférieur à 18 a été trouvé et il a été démontré que ce nombre était minimal.
Saurez-vous réaliser cet échange en moins de dix-huit mouvements ?
10 – Trois cercles sécants
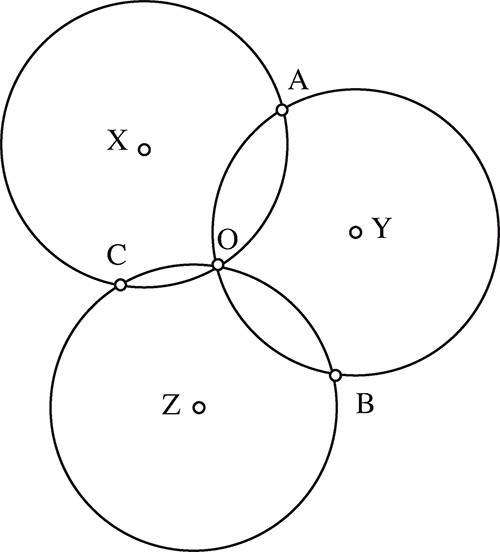
Trois cercles de rayon 1 dm passent par un point commun O.
Démontrez que les trois autres points d’intersection A, B et C sont situés sur un même cercle et déterminez le rayon de ce cercle.

