Les tresses les plus simples à réaliser ne nécessitent que trois brins (avec seulement deux brins, on ne peut réaliser qu’un enroulement, qui n’est pas une véritable tresse). Disposons ces brins verticalement : un brin gauche, un brin du milieu et un brin droit. Le schéma N représente la situation triviale de ces brins non tressés ; ce sera notre élément neutre.
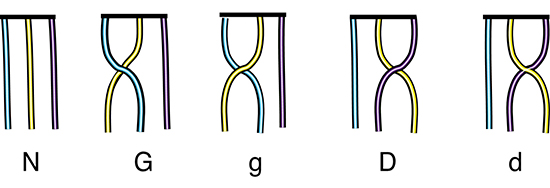
Dans ces schémas, on suppose que les brins sont fixés en haut et que les mouvements s’effectuent successivement avec les extrémités inférieures des brins.
En dehors du mouvement neutre N, les mouvements élémentaires possibles sont les suivants :
G : on passe le brin gauche sur le brin du milieu ;
g : on passe le brin gauche sous le brin du milieu ;
D : on passe le brin droit sur le brin du milieu ;
d : on passe le brin droit sous le brin du milieu.
On pourra ainsi coder un motif de tresse, composé d’une suite de mouvements, par un mot, par exemple GDGDGDGDGDG…, qui correspond au tressage traditionnel à trois brins.
Pour comparer deux tresses, il suffit de tendre les brins entre le haut et le bas. Deux tresses sont dites isotopes si l’on peut passer de l’une à l’autre en déformant continûment les brins sans les couper : elles appartiennent à la même classe d’équivalence. Ainsi, par exemple, les tresses dont les mots sont Gg et gG sont toutes les deux isotopes à la tresse neutre N, puisque, pour chacune, le second mouvement « annule » le premier. De même, les mots Dd, dD, GgGg, DdDd, GgDd… appartiennent à cette même classe neutre.
Les classes s’en mêlent
D’autres équivalences de mots, moins évidentes, peuvent être établies, par exemple DgD = GdG.
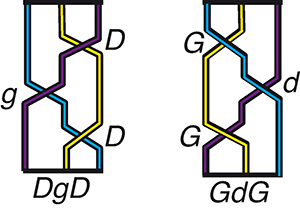
DgD = GdG, à un retournement haut/bas près.
Les classes d’isotopie de tresses à trois brins sont munies d’une opération qui consiste à accoler brin à brin les tresses résultant de mouvements élémentaires. Elles ont alors une structure de groupe, dont l’élément neutre est la tresse triviale (sans aucun croisement). Ce groupe compte une infinité d’éléments, la longueur des tresses n’étant pas limitée.
Le symétrique du mouvement D est le mouvement d : D–1 = d. De même, G–1 = g. Chaque élément du groupe possède donc un symétrique. L’opération qui consiste à accoler bout à bout les mouvements élémentaires est aussi, de façon naturelle, associative.
1. La loi de composition des tresses à trois brins est-elle commutative ?
Les artisans du cuir savent depuis longtemps réaliser une tresse à trois brins dans une bande de cuir comportant seulement deux incisions, sans séparer les extrémités des brins.
2. Comment passer de la tresse dénouée à la tresse nouée sans couper aucun brin ?


