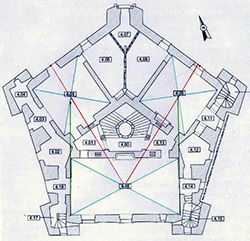
Plan du château de Maulnes, à Cruzy-le-Châtel (Yonne).
La triangulation d’un polygone, régulier ou non, se fait sans difficulté. On peut aussi disséquer un polygone en quadrilatères (« quadrilatérations » ?). Mais ici, ce sont les pentagones et les « pentagonations » qui nous intéresseront. Cela se fait également facilement si l’on n’impose aucune contrainte aux pièces du puzzle. En revanche, c’est plus délicat si l’on demande, par exemple, que les pièces soient toutes convexes.
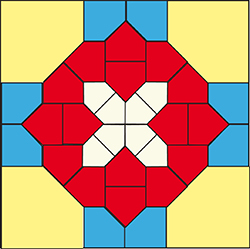
Ce découpage d’un carré en vingt-quatre pentagones convexes est l’œuvre du mathématicien et concepteur de puzzles américain Erich Friedman (né en 1965). Celui-ci s’est imposé des contraintes quant aux pentagones de son découpage : que ceux-ci soient réalisés à partir de carrés dont on a tronqué un ou deux angles et qu’ils ne présentent que des angles droits et des angles de 135°. Les pentagones sont de deux sortes. Les pentagones extérieurs, qu’Erich Friedmann appelle des couronnes, ont deux angles de 135° qui sont consécutifs ; les pentagones intérieurs, qu’Erich Friedmann appelle des assiettes, ont leurs angles de 135° qui ne sont pas consécutifs. Si l’on s’affranchit de la contrainte que les pièces s’obtiennent à partir de carrés tronqués, tout en gardant les contraintes des mesures d’angles et celle de la convexité, on peut s’inspirer de cette dissection pour découper un carré en un plus petit nombre de pentagones convexes.
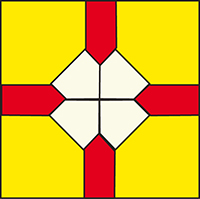
On a ici un découpage du carré en douze pentagones convexes. Mais si l’on n’impose plus aucune condition sur les angles, tout en gardant la convexité, on peut faire mieux.
Trouvez un découpage du carré en un nombre minimal de pentagones convexes.
Le triangle aussi… et les hexagones ?
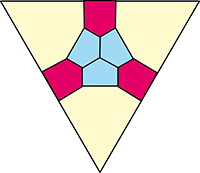
On peut aussi se demander en combien de pentagones convexes on peut découper un triangle. Voici un découpage du triangle en neuf pentagones convexes. Peut-on faire mieux ?
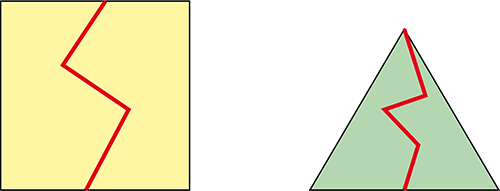
Si l’on abandonne la convexité, on peut évidemment découper un carré et un triangle en deux hexagones.
Mais c’est plus problématique si l’on impose que les pièces du découpage soient convexes. À l’heure actuelle, on ne connaît toujours pas de découpage du triangle ou du carré avec un nombre fini d’hexagones convexes. La question (ouverte) suivante est posée :
Est-ce possible avec un nombre fini d’hexagones convexes ? Et sinon, peut-on prouver l’impossibilité d’un tel découpage ?

