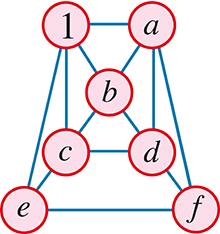
En 1512, le mathématicien italien Paolo Guarini di Forli publia un problème d’échange de cavaliers d’échecs sur un mini-échiquier de trois cases sur trois.

Il s’agissait d’échanger les deux cavaliers noirs et les deux cavaliers blancs. À chaque étape, un cavalier doit se déplacer sur une case vide en respectant la règle de déplacement d’un cavalier d’échecs (à savoir, selon la diagonale d’un rectangle de deux cases sur trois, dans n’importe quelle direction).
Dans son recueil Amusements in Mathematics de 1917, Henri Ernest Dudeney (1857–1930) reprend le même problème en citant Guarini, et en remplaçant les cavaliers par des grenouilles qui doivent effectuer des sauts analogues aux déplacements du cavalier d’échecs. Dans sa solution, le problémiste britannique expose une méthode qu’il appelle méthode des boutons et des fils.
La méthode se pratique de la façon suivante. Sur chaque case du mini-échiquier, à l’exception de la case centrale (qu’aucune grenouille ne peut atteindre), on place un bouton. Les huit boutons doivent pouvoir être différenciés, par une couleur, un matériau ou un numéro par exemple. Ensuite, en partant d’un premier bouton quelconque, on passe un fil qui relie ce premier bouton à un nouveau bouton accessible par un saut de cavalier, et on continue ainsi en passant le fil d’un bouton à un nouveau bouton jusqu’à éventuellement revenir au premier. Ensuite on « déplie » ce collier de boutons.

La solution apparaît alors de façon lumineuse ! En choisissant un sens de déplacement sur la boucle formée par le fil, on fait se déplacer tour à tour les grenouilles d’autant de cases qu’il le faut pour amener les grenouilles blanches sur les boutons initialement occupés par les noires, et les grenouilles noires sur les boutons initialement occupés par les blanches.
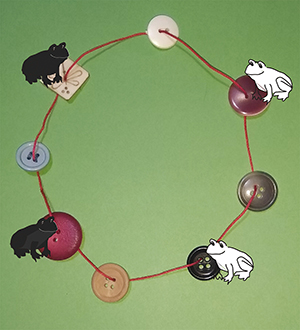
Dans la pratique, un simple diagramme vous rendra le même service que les boutons et le fil : inutile de vous ruer à la mercerie la plus proche !
Des grenouilles et des colliers de lettres

Voyons un autre problème à résoudre à l’aide d’un tel diagramme. En partant de A, qui est une voyelle, on avance de quatre lettres dans le sens de la flèche, et on arrive à la lettre E, qui est également une voyelle. On continue ensuite selon le principe suivant : si la lettre sur laquelle on est arrivé est une voyelle, on avance de quatre lettres dans le sens de la flèche ; si c’est une consonne, alors on recule de trois lettres.
En partant de X, qui est notre première lettre, quelle sera la deux mille vingt-deuxième lettre ?
Représentant le passage de chaque lettre à la suivante, on obtient le graphe suivant.
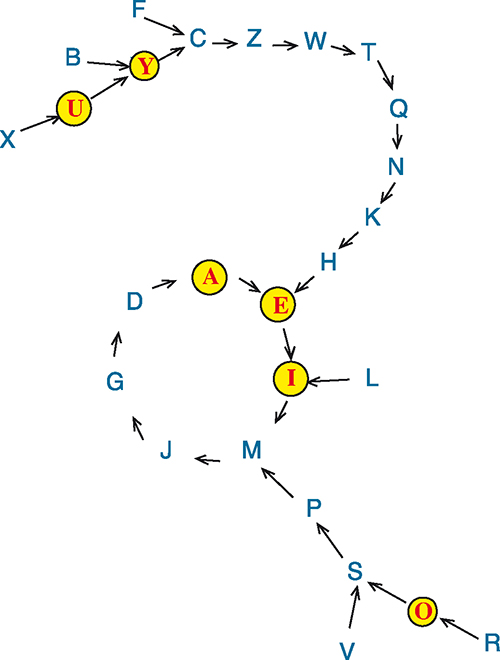
En partant de X, on atteint une boucle fermée après onze lettres. Cette boucle comprend sept lettres. En divisant 2022 – 11, soit 2011, par 7, on obtient un quotient entier de 287 et un reste égal à 2. On parcourra donc 287 fois la boucle de E à A, plus 2 lettres en partant de A : E et I. La réponse est donc I.
Voici enfin un dernier problème, pour lequel vous êtes invités à construire votre propre diagramme.
Placer les nombres de 2 à 7 dans les cases marquées d’une lettre (le 1 est déjà en place), de telle sorte que deux nombres consécutifs ne soient jamais situés dans deux cases directement reliées par un trait bleu.