
La spirale des fractions
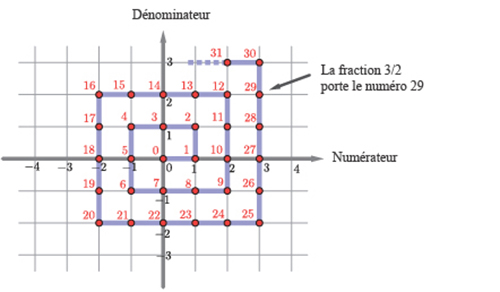
Pour remplacer une fraction par un entier, une méthode consiste à représenter chaque fraction n/d par le point de coordonnées (n, d), et à parcourir l’ensemble des points à coordonnées entières à l’aide d’une spirale comme ci-contre. Par exemple, la fraction 3/2 (correspondant au point (3, 2)) porte le numéro 29.
Cette méthode est classique pour démontrer que l’ensemble des nombres rationnels est dénombrable (c’est-à-dire, en un mot, qu’« il n’y a pas plus de fractions que d’entiers »). Elle est toutefois perfectible dans la mesure où des fractions différentes peuvent représenter le même nombre (par exemple, on a 3/2 = 6/4 = (-9)/(-6), etc.), et donc que des entiers différents peuvent en fait numéroter la même valeur.
Souder les nombres
Pour remplacer la paire numérateur-dénominateur par un entier unique, on peut aussi, en supposant tous les nombres positifs, procéder par recodage de leur écriture décimale. On peut par exemple écrire n en décimal, suivi de 00 (« soudure »), suivi de d en décimal, et remplaçant ensuite tous les 0 par des 01 (sauf ceux de la « soudure »). L’écriture obtenue est celle d’un entier k à partir duquel on peut facilement retrouver les valeurs n et d initiales, en retirant la « soudure » et ... Lire la suite gratuitement
