
Prenons une tarte et préparons-nous à la découper. On la partage d’abord en deux parts égales, on met de côté l’une des deux moitiés obtenues et on découpe l’autre, à nouveau en deux parts égales. À nouveau on en met une de côté et on partage l’autre en 2. Ensemble, les parts mises de côté représentent la somme et il reste une part représentant
pour compléter la tarte.
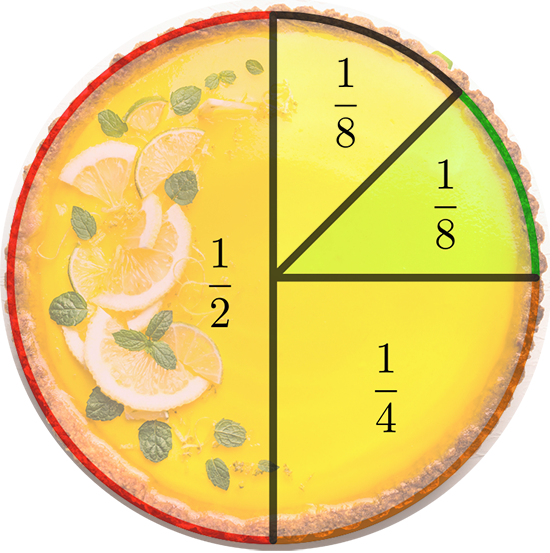
Découpage sans miette
Supposons que cette tarte ne fasse aucune miette et qu’on puisse la partager aussi longtemps que l’on veut, à chaque fois en découpant la part qui nous reste en deux parts égales et en en écartant une.
Après n partages, le morceau restant représentera de la tarte, ce que l’on peut écrire sous la forme
Ce morceau restant deviendra infiniment petit si l’on prolonge le processus, c’est-à-dire si n augmente indéfiniment. On a donc envie d’écrire que la somme infinie est égale à 1.
Une telle somme infinie, lorsqu’elle converge comme ici, s’appelle une série convergente, et sa limite se nomme la somme de la série.
Dans l’exemple de notre tarte, chaque nouveau morceau est la moitié ... Lire la suite
