« Votre commande est arrivée, Monsieur. »
Alpha s'empare de la boîte en carton que lui tend le robot-livreur avec un « Ah ! » de satisfaction. La soirée de révision dans la salle d'études de l'Institut intergalactique menace de s'éterniser et une petite pause pour contenter son estomac gargouillant est la bienvenue. Il ouvre le carton, une appétissante odeur de πzza pepperoni–fromage se répand dans la pièce.
« On partage ? » Le nez de Bêta n'a pas tardé à l'avertir de l'aubaine. Alpha accepte de bonne grâce. « Ok, je t'en donne la moitié. Il faut juste trouver un couteau pour la partager. »
« J'ai ce qu'il vous faut. » Le professeur Phi vient de se matérialiser devant les garçons ébahis. Sa tenue, une longue robe noire aux plis impeccables, ainsi que les zori en paille de riz qu'il porte à ses pieds, indiquent qu'il sort du dojo de l'Institut, où il s'entraîne quotidiennement. L'arme du jour bourdonne dans sa main : un sabre laser à l'éclat bleuté.
En quelques gestes souples et précis, il trace quatre traits de coupes sur la πzza au moyen de son sabre.
« Bon appétit » lance-t-il avec un sourire méphistophélique aux deux étudiants stupéfaits, avant de s'éclipser. « Comment va-t-on faire pour la partager équitablement ? grogne Bêta en considérant la πzza ravagée. Il l'a coupée n'importe comment…
– Pas tout à fait. »
C'est au tour d'Epsilon de faire son apparition à côté de la πzza, qui attire décidément beaucoup de monde.
La πzza au laser
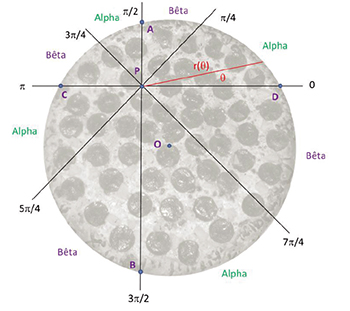
« Les quatre droites de coupe forment huit angles égaux de 45°, fait-elle remarquer. Imaginons qu'Alpha prenne une première part, puis Bêta la suivante, et ainsi de suite, en tournant autour du point d'intersection jusqu'à ce qu'il ne reste plus rien. Ça vous donnerait quelle quantité de πzza à chacun ? »
Devant le relatif manque d'enthousiasme de ses camarades pour les mises en équations, surtout lorsqu'elles impliquent des intégrales, la jeune fille s'empare d'un morceau de papier et enchaîne : « La surface de πzza dévolue à Alpha serait :
Bêta, lui, récupérerait :
– Mouais, marmonne Bêta, que tout cela laisse de marbre. Et alors ?
– Alors, l'expression sous l'intégrale a quelque chose de particulier. Tu pourras le constater en la calculant pour = 0 en fonction du rayon R de la πzza, c'est-à-dire, sur le schéma, PD2 + PA2 + PC2 + PB2. »
Cher lecteur, pouvez-vous calculer cette expression en fonction de R ? Et en déduire ce que l'on peut conclure concernant le partage de la πzza proposé par Epsilon ?