Supposons que les transports aient un coût fini sur terre, proportionnel à la distance parcourue, et que les transports sur mer aient un coût nul. Pour aller d'un point A à un autre point M d'une île, vaut-il mieux aller directement sur terre et parcourir le segment [AM] entre ces deux points, ou aller du point A par le plus court chemin à la côte, longer la côte sur mer puis remonter de la côte jusqu'au point d'arrivée M ? 

Jean-Pierre Kahane s'est intéressé au problème et l'a formulé ainsi :

« On se propose l'étude, en fonction de la forme de l'île, de l'ensemble K (A) des points M tels que le transport à moindre coût est réalisé par le parcours direct de A à M à l'intérieur de l'île. On s'intéresse à la famille des K (A) quand A parcourt l'intérieur de l'île. Premier exemple : l'île est de forme circulaire. La famille des ensembles K (A) est facile à décrire complètement. »

Le cas d'une île circulaire

En effet, pour une île circulaire, le lieu des points tels que ces deux trajets aient le même coût est une ellipse de foyers O et A, constructible avec le procédé du jardinier (voir ci-dessous).

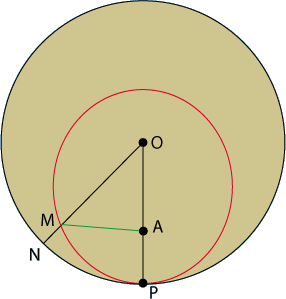
Le principe en est simple : on cherche les points M de l'île tels que AM = AP + MN où P est le point (fixe) de la côte le plus proche de A et N le point (variable) le plus proche de M. En appelant O le centre de l'île et r son rayon, cela donne : 

AM = AP + (r – OM), soit AM + OM = k, avec k = AP + r.

Ainsi, M est situé sur l'ellipse de foyers A et O passant par P.

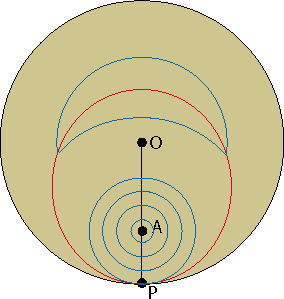
On peut aussi s'interroger sur l'allure des courbes décrites par les points équidistants du point de départ. Près du point A ce sont des cercles concentriques, puis deux arcs de cercles quand les cercles concentriques interceptent l'ellipse.

 Le cas d'un continent

Jean-Pierre Kahane poursuit : « Second exemple : on transforme un peu la question. Au lieu d'une île, qui est un disque dans le premier exemple, on considère un continent dont le bord sur la mer est parfaitement rectiligne, c'est-à-dire un demi-plan. Le problème du moindre coût se pose de la même façon. Là encore, on peut définir les ensembles K(A) et les décrire complètement. »

Sauriez-vous démontrer, comme l'indique Jean-Pierre Kahane, que pour le demi-plan, l'ensemble des points K (A) est une parabole ?

Ce cas est à la base du troisième exemple cité par Jean-Pierre Kahane, quand l'île est un polygone convexe. L'ensemble K (A) est constitué de fragments de paraboles.

Les généralisations à des coûts non nuls mais inférieurs sur mer seraient plus réalistes, mais moins belles « géométriquement ».