Médiatrices dans le taxi-plan

Constitué d'un réseau de routes, le taxi-plan comporte des blocs carrés d'immeubles de côté une unité (1 hectomètre), des rues illimitées orientées d'Est en Ouest et des avenues sans fin orientées du Sud au Nord. Les distances dans ce plan ne sont pas les distances « à vol d'oiseau » usuelles, mais les distances que parcourrait un taxi en empruntant le chemin le plus court (ou l'un des chemins les plus courts) par le réseau des routes.

Quelles sont les diverses formes que peut prendre la médiatrice d'un bipoint dans le taxi-plan ? On parle de bipoint et non de segment : dans le cas où deux points A et B sont situés sur une même route, le segment [AB] correspond au segment de même nom dans le plan euclidien, mais il n'est pas possible de définir un segment dans le cas contraire. La médiatrice d'un bipoint {A, B} est l'ensemble des points équidistants de A et B, la distance étant ici la taxi-distance, c'est-à-dire la distance minimale parcourue par un taxi pour se rendre de A à B. On se limitera ici à des points situés à des intersections de rues et d'avenues, mais on pourrait étendre l'étude à des points quelconques du réseau.

Le segment [AB] est bien défini, mais on ne peut pas définir un segment d'extrémités B et C ou A et C.

Lorsque deux points appartiennent à une même route, deux cas sont à considérer. Si les deux points sont placés symétriquement de part et d'autre d'une avenue (comme A et B sur le schéma suivant), cette avenue est la médiatrice du bipoint {A, B}. Si les deux points ne sont pas placés symétriquement de part et d'autre d'une avenue (comme les points B et C), la médiatrice Δ _{{B, C}} sera constituée de points isolés.

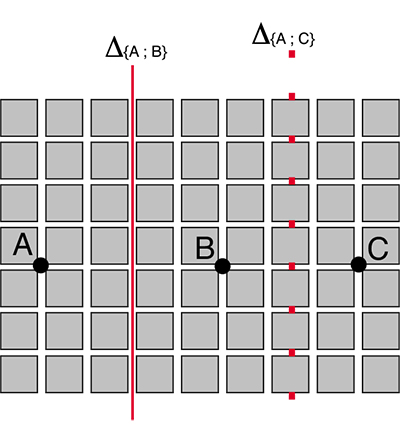
La médiatrice de deux points appartenant à une même route : les deux cas possibles.

Lorsque deux points n'appartiennent ni à une même rue, ni à une même avenue, cela se complique un peu. Plaçons-nous déjà dans le cas où la droite (AB) n'est pas parallèle à une diagonale des blocs. Ici encore, si les points sont des intersections de rues et d'avenues, deux cas sont à distinguer selon que la taxi-distance entre les deux points est un nombre entier pair ou impair d'hectomètres. Dans le cas pair, la médiatrice est la réunion de deux demi-droites et de points isolés « reliant » les origines de ces demi-droites. Dans le cas impair, la médiatrice est un ensemble de points isolés.

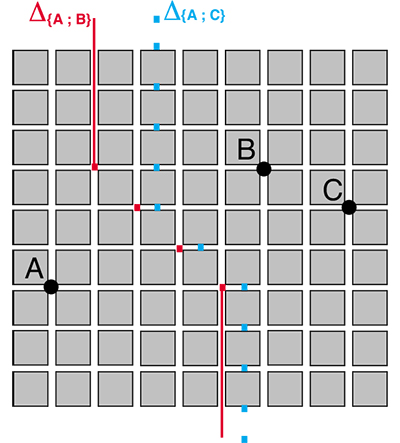
La médiatrice de deux points n'appartenant pas à une même route, le bipoint n'étant pas orienté à 45° par rapport aux routes : les deux cas possibles.
Les points A, B et C ne sont pas alignés, mais les deux médiatrices Δ_{A, B} et Δ_{A, C} ont une intersection vide !

Le cas le plus étonnant est celui où les deux points sont orientés à 45° par rapport aux rues et aux avenues. M.C.

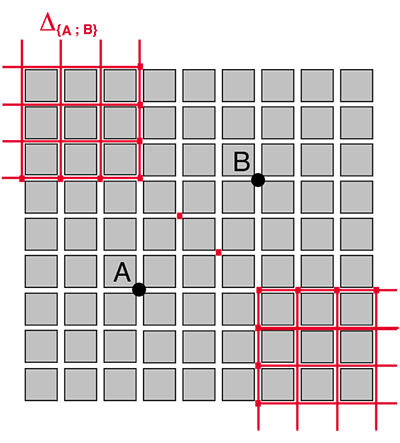
La médiatrice est constituée de la réunion de points isolés et de « quarts de taxi-plans ».