Un philanthrope, Sir Pinsky, décide de construire un musée. Passionné de mathématiques, il décide d’établir le plan de l’édifice en n’utilisant que les notions de milieu et de triangle équilatéral. Plus précisément, à chaque étape de la construction, il prend les milieux des côtés des triangles « orientés vers le haut » afin de construire de nouveaux triangles, comme d’après les schémas ci-dessous.
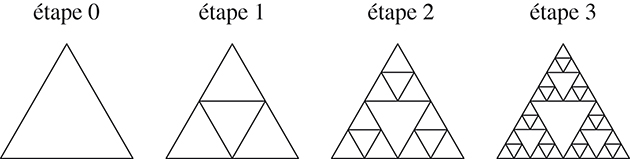
Une pièce doit ainsi pouvoir communiquer directement avec toutes les pièces voisines.
On s’intéresse au nombre de portes intérieures que comporte l’édifice (les portes sont installées au milieu des murs de chaque pièce).
Par exemple, s’il s’arrêtait à la première étape, il y aurait trois portes intérieures (voir le schéma suivant), mais s’il s’arrêtait à la deuxième étape, il y aurait quinze portes intérieures.
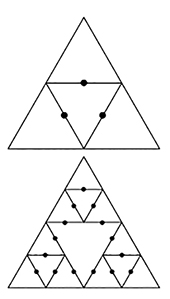
Combien de portes intérieures comportera l’édifice s’il s’arrête à la septième étape ?

